
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{\sqrt{AC^2+\left(v_n.\dfrac{t_1}{2}\right)^2}}{v}=1\)
\(\Rightarrow AC^2+v^2_n.\dfrac{t^2_1}{4}=v^2\)
\(\Rightarrow v_n^2.\dfrac{t^2_1}{4}=v^2-AC^2\)
\(\Rightarrow t_1^2=\dfrac{4\left(v^2-AC^2\right)}{v_n^2}\Rightarrow t_1=\dfrac{2\sqrt{v^2-AC^2}}{v_n}\)
Theo tao muốn chuyển đổi vậy thì :
\(\dfrac{\sqrt{AC^2+\left(v_n.\dfrac{t_1}{2}\right)^2}}{v}=\dfrac{1}{2}t_1\)
\(\Leftrightarrow\dfrac{\sqrt{AC^2+v_n^2.\dfrac{t_1^2}{4}}}{v}=\dfrac{1}{2}t_1\)
\(\Leftrightarrow\dfrac{\sqrt{\dfrac{4AC^2+\left(v_n.t_1\right)^2}{4}}}{v}=\dfrac{1}{2}t_1\)
\(\Leftrightarrow\dfrac{\sqrt{4AC^2+\left(v_n.t_1\right)^2}}{2v}=\dfrac{1}{2}t_1\)
\(\Leftrightarrow t_1=\dfrac{\sqrt{4AC^2+\left(v_n.t_1\right)^2}}{v}\)
\(\Leftrightarrow t_1v=\sqrt{4AC^2+\left(v_n.t_1\right)^2}\)
\(\Leftrightarrow t_1^2.v^2=4AC^2+v_n^2.t^2_1\)
\(\Leftrightarrow t_1^2\left(v^2-v^2_n\right)=4AC^2\)
\(\Leftrightarrow t_1^2=\dfrac{4AC^2}{v^2-v_n^2}\)
\(\Leftrightarrow t_1=\dfrac{2AC}{\sqrt{v^2-v_n^2}}\)
Are you OK??? :D

Vì I,K là trung điểm AD,BC nên \(2IK=AB+CD\)
\(\Rightarrow60=2x+x\\ \Rightarrow x=20\)

Vì tổng số trận đấu là 10 trận khi đó \(\frac{x(x-1)}{2}=10\)
Ta có : \(\frac{x(x-1)}{2}=10\)
\(\Rightarrow x(x-1)=10\cdot2\)
\(\Rightarrow x(x-1)=20\)
Do 20 = 4.5 nên có 5 đội tham gia thi đấu


Trả lời nhiều vào :)
Nhưng câu trả lời phải mang tính thuyết phục và có lí.
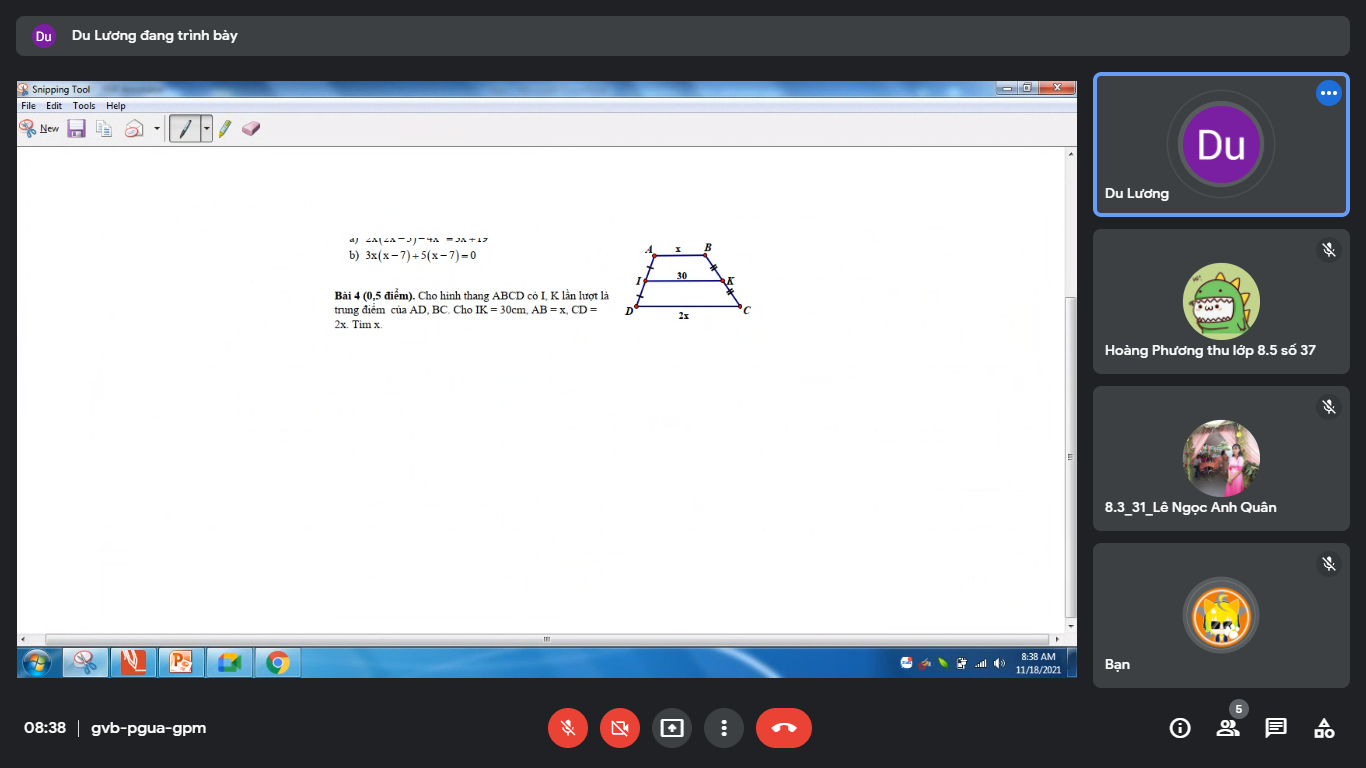 mọi người làm chi tiết ra đc ko vậy mn cảm ơn mn.
mọi người làm chi tiết ra đc ko vậy mn cảm ơn mn.
Olm chào em, hiện tại hệ thống đang update nên phần thi đấu chưa vào được. Cảm ơn em đã đồng hành cùng Olm. Chúc em học tập hiệu quả và vui vẻ cùng Olm.
chắc tk bạn lỗi rồi, đăng xuất vào lại xem sao nha.