Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

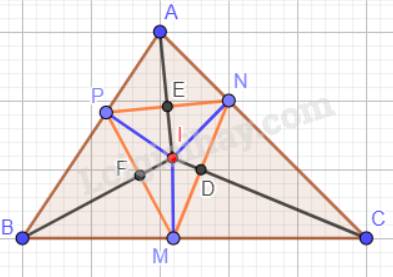
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.

B D H I A N M C
a,Vì :
\(AM\mp BC,CI\)\(\Omega\)\(AD,CI\)\(\Omega\)\(AM=N\)
\(\rightarrow N\)là trực tâm \(\Delta ADC\rightarrow DN\)\(\Omega\)\(AC\)
b,Vì :
\(\widehat{BAC}=45^O,\frac{BM}{BA}=\frac{1}{\sqrt{2}}\rightarrow\Delta ABM\) vuông cân tại \(M\)
\(\rightarrow\Delta ABC\) vuông cân tại \(A\)
\(\rightarrow AB=AC\)MÀ
\(\widehat{BAH}=\widehat{ACI}\left(+\widehat{DAC}=90^O\right),\widehat{AHB}\)
\(=\widehat{AIC}=90^O\)
\(\rightarrow\Delta ABH=\Delta CAI\left(g,c,g\right)\)
\(\rightarrow BH=AI\rightarrow BH^2+CI^2=AI^2+CI^2=AC^2=AB^2=2BM^2=\frac{BC^2}{2}=const\)
c,Ta có
\(\widehat{AIC}=\widehat{NMC}=90^O\rightarrow\widehat{IAN}=\widehat{NCM}\)
\(\rightarrow\Delta AIN~\Delta CMN\left(g.g\right)\rightarrow\frac{AN}{CN}=\frac{IN}{MN}\)
\(\rightarrow\Delta NIM~\Delta NAC\left(c.g.c\right)\rightarrow\widehat{MIN}=\widehat{NAC}=45^O\)Mà:
\(CI\) ! \(ID\rightarrow IM\)Là phân giác \(\widehat{CIH}\)\(\rightarrow\)Tia phân giác của góc HIC luôn đi qua 1 điểm M cố định.
Lưu ý : \(\mp\)Thay cho !
\(\Omega\)thay cho
NHiều công thức mk ko thấy nên là mk viết thay bằng cái khác tương tự xíu nha bn
Dữ kiện đề bài:
Các bước vẽ hình:
Minh họa sơ đồ bằng mô tả ASCII đơn giản:
Nếu bạn muốn hình vẽ:
Tôi có thể vẽ hình đúng theo mô tả cho bạn. Bạn muốn tôi vẽ hình ngay bây giờ chứ?