Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số cần tìm là abcde ( e chẵn và các chữ số khác nhau từng đôi một )
TH1 : e = 0
Chọn e : 1 cách
Chọn a :5 cách
chọn b :4 cách
chọn c :3 cách
chọn d :2 cách
=> Theo Quy tắc nhân có : 1.5.4.3.2 = 120 .
TH2 : e # 0
Chọn e :2 cách
Chọn a :4 cách
chọn b :4 cách
chọn c :3 cách
chọn d :2 cách
=> Theo quy tắc nhân có :2.4.4.3.2 = 192
=> Có tất cả 192 +120 =312 số chẵn có 5 chữ số khác nhau
-
Số tự nhiên đó có dạng \(\overline{abcde}\)
a, a có 5 cách chọn.
b có 5 cách chọn.
c có 4 cách chọn.
d có 3 cách chọn.
e có 2 cách chọn.
\(\Rightarrow\) Có \(5.5.4.3.2=600\) số thỏa mãn.
b, TH1: \(e=0\)
a có 5 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2=120\) số thỏa mãn.
TH2: \(e\ne0\)
a có 5 cách chọn.
e có 2 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2.2=240\) số thỏa mãn.
Vậy có \(120+240=360\) số tự nhiên thỏa mãn yêu cầu bài toán.
c, TH1: \(e=0\Rightarrow\) có 120 số thỏa mãn.
TH2: \(e=5\)
a có 4 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(4.4.3.2=96\) số thỏa mãn.
Vậy có \(120+96=216\) số tự nhiên thỏa mãn yêu cầu bài toán.
Ta "dán" 2 chữ số 3 và 3 liền với nhau thành chữ số kép. Có hai cách "dán" (23 hoặc 32). Bài toán trở thành: có 5 chữ số 0,1,4,5, số kép. Hỏi có thể lập được bao nhiêu số tự nhiên mỗi số có 5 chữ số khác nhau.
Ta giải bằng quy tắc nhân như sau:
Bước 1: Dán 2 số 2 và 3 với nhau. Có \(n_1\) = 2 cách
Bước 2: Số hàng vạn có \(n_2\) = 4 cách chọn (trừ số 0)
Bước 3: Số hàng nghìn có \(n_3\) = 4 cách chọn
Bước 4: Số hàng trăm có \(n_4\) = 3 cách chọn
Bước 5: Số hàng chực có \(n_5\) = 2 cách chọn
Bước 6: Số hàng đơn vị có \(n_6\) = 1 cách chọn
Theo quy tắc nhân số các số cần chọn là
n = \(n_1\)\(n_2\)\(n_3\)\(n_4\)\(n_5\)\(n_6\) = 2.4.4.3.2.1 = 192
Vậy có 192 số cần tìm.
Gọi tập hợp E = {0,1,2,3,4,5}
c) Số tự nhiên có 3 chữ số có dạng
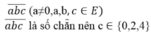
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3*6*5 = 90 số có 3 chữ số.
Vì vậy đáp án là B
Ta có 5 cách chọn hàng chục và bốn cách chọn hàng đơn vị nên ta có 4*5=20 số
Đặt y=23, xét các số 
trong đó a;b;c;d;e đôi một khác nhau và thuộc tập {0;1;y;4;5}.
Khi đó có 4 cách chọn a; 4 cách chọn b; 3 cách chọn c; 2 cách chọn d và 1 cách chọn e.
Theo quy tắc nhân có 4.4.3.2=96 số
Khi ta hoán vị trong y ta được hai số khác nhau
Nên có 96.2=192 số thỏa yêu cầu bài toán.
Chọn A.
Đáp án A
Gọi số cần tìm có dạng 
Chọn a : có 2 cách
Chọn b, c : có 
cách
Vậy có 
số.
Số tận cùng chẵn: 0, 2, 4 (3 số)
Hàng trăm: không 0, khác tận cùng
Hàng chục: khác 2 số kia
Tính:
Cuối \(0\) → \(5 × 4 = 20\)
Cuối \(2\) → \(4 × 4 = 16\)
Cuối \(4\) → \(4 × 4 = 16\)
Tổng \(= 20 + 16 + 16 = 52\) số.
cho hình tam giác ABC diện tích là 60cm2 trên v=cạnh BC lấy điểm M sao cho MD = MC nối A với M trên AM lấy diểm D sao cho MD=1/3AM kéo dài đoạn BD cắt AC hãy chứng tỏ AN=NC