Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
Suy ra: \(\widehat{ABO}=\widehat{ACO}=90^0\)
hay AC là tiếp tuyến của (O)
b: Xét (O) có
OI là một phần đường kính
CE là dây
OI⊥CE tại I
Do đó: I là trung điểm của CE
Xét ΔDCE có
DI là đường cao
DI là đường trung tuyến
Do đó: ΔDCE cân tại D
Xét ΔOED và ΔOCD có
OE=OC
ED=CD
OD chung
Do đó: ΔOED=ΔOCD
Suy ra: \(\widehat{OED}=\widehat{OCD}=90^0\)
hay DE là tiếp tuyến của (O)

a, (O): góc BAC=90 độ (góc nt chắn nửa đường tròn).
(I): góc AEH=90(góc nt chắn nửa đường tròn). góc ADH=90(góc nt chắn nửa đường tròn) => tg AEHD là hcn(có 3 góc vuông)
b) (I): góc ADE=góc AHE( nt cùng chắn cung AE)
ta lại có:góc AHE=góc ABH( cùng phụ với góc BAH.) => ADE=ABH
=> tg BEDC nội tiếp (góc trong tại 1 đỉnh = góc ngoài tại đỉnh đối diện)
c, tg AEHD là hcn; AH cắt AD tại I => IA=IH=IE=ID
tam giác ADH: DI là trung tuyến
tam giác: AMH: MI là trung tuyến => D,M,I thẳng hàng. mà E,M,I thẳng hàng=> D,M,E thẳng hàng.
Nhớ L I K E nha

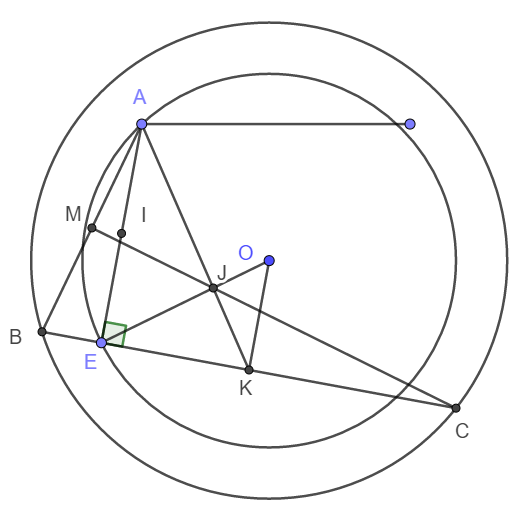
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

Vì cung ACAC có số đo 50∘50∘ nên ˆAOC=50∘AOC^=50∘
Vì AO⊥CD;AO//DE⇒CD⊥DEAO⊥CD;AO//DE⇒CD⊥DE⇒ˆCDE=90∘⇒CDE^=90∘ mà C,D,E∈(O)C,D,E∈(O) nên CECE là đường kính hay C;O;EC;O;E thẳng hàng
Xét (O)(O) có OAOA là đường cao trong tam giác cân ODCODC nên OAOA cũng là đường phân giác ⇒ˆCOA=ˆAOD=50∘⇒COA^=AOD^=50∘
Lại thấy ˆBOE=ˆAOC=50∘BOE^=AOC^=50∘ (đối đỉnh) suy ra ˆAOC=ˆAOD=ˆBOE=50∘AOC^=AOD^=BOE^=50∘ (D đúng) và suy ra cung ACAC bằng cung BEBE nên B đúng.
Ta có ˆDOE=180∘−ˆAOD−ˆBOE=80∘DOE^=180∘−AOD^−BOE^=80∘ nên cung AD<AD< cung DE⇒AD<DEDE⇒AD<DE hay đáp án A sai.
Lại có ˆAOE=ˆAOD+ˆDOE=50∘+80∘=130∘AOE^=AOD^+DOE^=50∘+80∘=130∘ và ˆBOD=ˆBOE+ˆDOE=50∘+80∘=130∘BOD^=BOE^+DOE^=50∘+80∘=130∘
Nên ˆAOE=ˆBODAOE^=BOD^ suy ra số đo cung AE=AE= số đo cung BD.BD. Do đó C đúng.
Phương án B, C, D đúng và A sai.

Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)


a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>BC⊥ DA tại C
Xét tứ giác ACHM có \(\hat{HCA}+\hat{HMA}=90^0+90^0=180^0\)
nên ACHM là tứ giác nội tiếp
=>A,C,H,M cùng thuộc một đường tròn
b: Xét ΔMBH vuông tại M và ΔMDA vuông tại M có
\(\hat{MBH}=\hat{MDA}\left(=90^0-\hat{DAB}\right)\)
Do đó: ΔMBH~ΔMDA
=>\(\frac{MB}{MD}=\frac{MH}{MA}\)
=>\(MB\cdot MA=MH\cdot MD\)
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE⊥ DB tại E
Xét ΔDAB có
BC,DM là các đường cao
BC cắt DM tại H
Do đó: H là trực tâm của ΔDAB
=>AH⊥DB
mà AE⊥ DB
và AH,AE có điểm chung là A
nên A,H,E thẳng hàng
a) Chứng minh 4 điểm A, C, H, M cùng thuộc một đường tròn
Chứng minh:
Giờ xét tam giác \(A C H\) và điểm \(M\):
Dễ thấy: \(\angle A H M = \angle A C M\), do cùng chắn cung \(A M\) trên đường tròn có đường kính AB.
Nhưng để chặt chẽ hơn:
Cách làm chuẩn hơn:
b) Gọi E là giao điểm của BD với đường tròn (O), E khác B. Chứng minh:
(1) MA·MB = MD·MH
Gợi ý: Ta chứng minh hai tam giác đồng dạng hoặc sử dụng tính chất giao điểm của hai dây cung.
Tuy nhiên, điểm M không nằm trên đường tròn (O), nên ta xét đường tròn qua A, C, H, M (tứ giác nội tiếp đã chứng minh ở câu a).
Suy ra từ định lý giao điểm hai dây cung:
\(M A \cdot M B = M D \cdot M H\)
Vì các điểm A, H, C, M cùng thuộc một đường tròn.
(2) Ba điểm A, H, E thẳng hàng
Ta chứng minh \(A , H , E\) thẳng hàng.
Ta chứng minh điều này qua tam giác vuông hoặc định lý góc nội tiếp bằng nhau.
Một cách tiếp cận:
→ Từ đó ta chứng minh được 3 điểm A, H, E thẳng hàng.
Vẽ hình minh họa chi tiết:
Ta sẽ mô tả các bước để bạn vẽ tay hoặc bằng phần mềm như GeoGebra: