Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)

V trụ=15*3^2*pi=135pi
V nón=1/3*pi*3^2*8=24pi
=>V=159pi

Do chiều cao gấp 3 lần đường kính nên chiều cao gấp 6 lần bán kính
Hay \(h=6R\)
Áp dụng công thức diện tích toàn phần:
\(2\pi R^2+2\pi Rh=7\pi\)
\(\Rightarrow2R^2+2R.6R=7\)
\(\Rightarrow14R^2=7\)
\(\Rightarrow R=\dfrac{\sqrt{2}}{2}\) \(\Rightarrow h=6R=3\sqrt{2}\)
Thể tích: \(V=\pi R^2h=\dfrac{3\pi\sqrt{2}}{2}\)

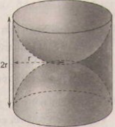
Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
Sxq = 2πrh = 2πr.2r = 4πr2
Diện tích mặt cầu:
S = 4πr2
Diện tích cần tính là:
4πr2 + 4πr2 = 8πr2

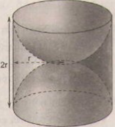
Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
S xq = 2 π rh = 2 π r ⋅ 2 r = 4 π r 2
Diện tích mặt cầu:
S = 4 π r 2
Diện tích cần tính là:
4 π r 2 + 4 π r 2 = 8 π r 2
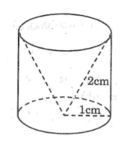

Để tính diện tích xung quanh của hình nón, ta dùng công thức:
\(S_{x q} = \pi r l\)
Trong đó:
Theo đề bài:
Giả sử:
Vậy:
\(l = \sqrt{r^{2} + h^{2}}\)
Suy ra:
\(S_{x q} = \pi r \sqrt{r^{2} + h^{2}}\)
✅ Kết luận:
Diện tích xung quanh của hình nón là:
\(\boxed{\pi r \sqrt{r^{2} + h^{2}}}\)
Cô giúp con giải bài toán về hình trụ và hình nón này nhé!
Đề bài tóm tắt:
Công thức cần nhớ:
\(S = \pi r l\)
với
\(r\) = bán kính đáy
\(l\) = độ dài đường sinh (đường tạo thành bên hông nón).
\(l = \sqrt{r^{2} + h^{2}}\)
Áp dụng:
\(l = \sqrt{r^{2} + h^{2}}\)
\(S = \pi r \sqrt{r^{2} + h^{2}}\)
Nếu con có số liệu cụ thể về \(r\) và \(h\), cô có thể giúp tính luôn số liệu cụ thể nhé!