Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây toán lớp 9, ko phải toán 7 nha!
B C A O M N K H I
(O) tiếp xúc AB;AC lần lượt tại H;K
\(S_{AMN}=S_{OAM}+S_{OAN}=\frac{1}{2}OH.AM+\frac{1}{2}OK.AN=\frac{AM+AN}{2}\)
Vẽ \(MI\perp AC;I\in AC\)
Ta có: \(AM\ge MI\)
Áp dụng bất đẳng thức Côsi cho hai số không âm , ta có:
\(\frac{AM+AN}{2}\ge\sqrt{AM.AN}\)
Do đó :\(S_{AMN}\ge\sqrt{AM.AN}\ge\sqrt{MI.AN}\)
Ta có: \(S_{AMN}\ge\sqrt{2S_{AMN}}\Leftrightarrow S^2_{AMN}\ge2S_{AMN}\Leftrightarrow S_{AMN}\ge2\)
Dấu " = " xảy ra \(\Leftrightarrow I=A\Leftrightarrow MN\perp OA;\widehat{BAC}=90^0\)
Giá trị nhỏ nhất của diện tích tam giác AMN là 2

Tâm đường tròn nội tiếp tam giác đều là giao điểm của ba đường trung trực của tam giác đó.
Vẽ hai đường trung trực của tam giác đều, giao điểm của đường trung trực chính là tâm đường tròn nội tiếp ta giác đều

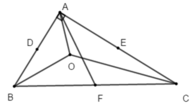
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D

Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
Tâm đường tròn ngoại tiếp tam giác là giao của 3 đường trung trực nha bạn
còn giao của 3 đường phân giác là tâm đường tròn nội tiếp tam giác nha
nếu hai cái tâm đó trùng nhau thì chỉ có tam giác đều thôi
Em xác định giao 3 đường trung trực nhé. Vì tính chất giao 3 đường trung trực cách đề 3 đỉnh của tam giác, nên đó sẽ là tâm đường tròn ngoại tiếp tam giác.