Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ dài cạnh là \(\sqrt{32}=4\sqrt{2}\left(cm\right)\)
Diện tích xung quanh của hình lập phương là:
\(4\cdot\left(4\sqrt{2}\right)^2=4\cdot32=128\left(cm^2\right)\)

Giải:
Diện tích xung quanh : 16.4 =64 m\(^2\)
Diện tích toàn phần : 16.6 =96 m\(^2\)
Độ dài 1 cạnh là \(\sqrt{16}=4\left(m\right)\)
Diện tích xung quanh là 4^2*4=64(m2)
Diện tích toàn phần là: 4^2*6=96m2

Độ dài cạnh của hình lập phương là \(\sqrt[3]{729}=9\left(cm\right)\)
Diện tích xung quanh của hình lập phương là \(4.9^2=324\left(cm^2\right)\)
Diện tích toàn phần của hình lập phương là \(6.9^2=486\left(cm^2\right)\)
Thể tích của hình lập phương đề bài đã cho là \(729cm^3\)
Lớp 7 đã học dạng \(\sqrt[3]{729}\) đâu nhỉ, theo em nên viết:
Vì \(9\cdot9\cdot9=729\) nên cạnh hình vuông là 9cm

Vì \(9^2+12^2=15^2\) nên ở đáy là tam giác vuông.
Diện tích mặt đáy là:
\(\dfrac{9\cdot12}{2}=54\left(m^2\right)\)
Chu vi mặt đáy là:
\(9+12+5=26\left(m\right)\)
Diện tích xung quanh lăng trụ:
\(26\cdot5=130\left(m^2\right)\)
Diện tích toàn phần lăng trụ:
\(130+54\cdot2=238\left(m^2\right)\)
Thể tích lăng trụ:
\(54\cdot5=270\left(m^3\right)\)

`1,`
S một đáy của hình lập phương đó là:
`144 \div 4 = 36 (m^2)`
Độ dài cạnh của hình lập phương đó là:
\(\sqrt {36} = 6(m)\)
Vậy, độ dài cạnh của hình lập phương đó là `6 m`.
`2,`
P đáy của hình hộp chữ nhật đó là:
`2(5+6)=2*11=22(m^2)`
Chiều cao của hình hộp chữ nhật đó là:
`154 \div 22=7 (m)`
Vậy, độ dài của chiều cao hình hộp chữ nhật đó là `7m.`

Diện tích xung quanh hình lập phương là: \(S = 4{a^2}\)
\(\begin{array}{l} \Rightarrow 100 = 4{a^2}\\ \Rightarrow {a^2} = 100:4\\ \Rightarrow a = 5\left( {cm} \right)\end{array}\)
Thể tích hình lập phương đó là:
\(V = {a^3} = {5^3} = 125\left( {{m^3}} \right)\)

Vì là \(a^3\) nên mình dùng nthe ;-; với lại cũng có học căn nên mình làm vậy, còn nếu mà không được thì cho mình sửa:
Thể tích của hình lập phương đó là \(125m^3\)
Mà \(125=5^3\)
\(\Rightarrow\) Độ dài 1 cạnh của hình lập phương đó là \(5m\)
Độ dài cạnh là \(\sqrt[3]{125}=5\left(m\right)\)
Diện tích xung quanh là:
5^2*4=100(m2)

a)
Diện tích xung quanh khối gạch hình lập phương là :
4 . 202 = 1600 (cm2)
Diện tích toàn phần của khối gạch hình lập phương là:
\({6.20^2} = 2400\left( {c{m^2}} \right)\)
b)
Theo hình vẽ ta ta có:
Chiều rộng của viên gạch hình hộp chữ nhật bằng \(\dfrac{1}{2}\) cạnh hình lập phương
Chiều rộng của hình hộp chữ nhật là: 20 : 2=10 (cm)
Chiều cao của viên gạch bằng \(\dfrac{1}{4}\) cạnh hình lập phương
Chiều cao của viên gạch là:20 : 4 = 5 (cm)
Vậy mỗi viên gạch có kích thước là: chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm.

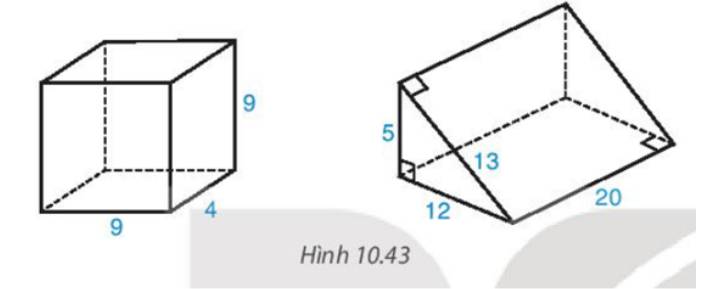
Diện tích xung quanh hình hộp chữ nhật là : \(2.\left( {4 + 9} \right).9 = 234\)
Diện tích toàn phần hình hộp chữ nhật là: \(234 + 2.9.4 = 306\)
Thể tích hình hộp chữ nhật là: \(9.4.9 = 324\)
Diện tích xung quanh hình lăng trụ là :\(\left( {5 + 12 + 13} \right).20 = 600\)
Diện tích toàn phần hình lăng trụ là:\(600 + 2.\dfrac{1}{2}.5.12 = 660\)
Thể tích hình lăng trụ là: \(\left( {\dfrac{1}{2}.5.12} \right).20 = 600\)
1. Diện tích đáy (A₀) của hình lập phương:
Diện tích đáy là diện tích của một mặt vuông của hình lập phương. Ta có:
\(A_{0} = a^{2}\)
Trong đó, \(a\) là độ dài cạnh của hình lập phương.
2. Tính cạnh của hình lập phương:
Biết diện tích đáy \(A_{0} = 32 \textrm{ } m^{2}\), ta có thể tìm cạnh của hình lập phương:
\(a^{2} = 32 \Rightarrow a = \sqrt{32} = 4 \sqrt{2} \approx 5.656 \textrm{ } m\)
3. Diện tích xung quanh (A_x):
Diện tích xung quanh của hình lập phương là diện tích của 4 mặt bên. Công thức tính là:
\(A_{x} = 4 a^{2}\)
Thay \(a^{2} = 32\), ta có:
\(A_{x} = 4 \times 32 = 128 \textrm{ } m^{2}\)
4. Diện tích toàn phần (A_t):
Diện tích toàn phần của hình lập phương là tổng diện tích của 6 mặt. Công thức tính là:
\(A_{t} = 6 a^{2}\)
Thay \(a^{2} = 32\), ta có:
\(A_{t} = 6 \times 32 = 192 \textrm{ } m^{2}\)
5. Thể tích (V):
Thể tích của hình lập phương được tính bằng:
\(V = a^{3}\)
Thay \(a = 4 \sqrt{2}\), ta có:
\(V = \left(\right. 4 \sqrt{2} \left.\right)^{3} = 4^{3} \times \left(\right. \sqrt{2} \left.\right)^{3} = 64 \times 2 \sqrt{2} = 128 \sqrt{2} \approx 181.019 \textrm{ } m^{3}\)
Tóm lại: