K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MN
1
18 tháng 11 2016
ĐK: -1<x\(\ne\)0
Đặt \(log_3\left(x+1\right)=t\) (t\(\ne\)0)
bpt trở thành \(\frac{1}{3^t}>\frac{1+t}{3^t-1}\)
\(\Leftrightarrow\frac{1+t}{3^t-1}-\frac{1}{3^t}< 0\Leftrightarrow\frac{t.3^t+1}{3^t\left(3^t-1\right)}< 0\)
vì \(3^t>0\forall t\) nên ta có thể nhân 2 vế của bpt với \(3^t\)
Khi đó, ta có bpt \(\Leftrightarrow\frac{t.3^t+1}{3^t-1}< 0\)
*) Đặt \(f\left(t\right)=t.3^t+1\), f(0)=1
dễ thấy f(t) đồng biến trên tập R
*) Xét 2 trường hợp:
+TRƯỜNG HỢP 1) với t<0 \(\Leftrightarrow3^t< 1\Leftrightarrow3^t-1< 0\) (1)
vì \(\lim\limits_{t\rightarrow-\infty}\left[f\left(t\right)\right]=1\) nên f(t)>1 với mọi t \(\Leftrightarrow t.3^t+1>1\Rightarrow t.3^t+1>0\forall t\) (2)
kết hợp (1) và (2) ta thấy t<0 thỏa mãn bpt
+TRƯỜNG HỢP 2) với t>0 \(\Leftrightarrow3^t-1>0\) (3)
lại có f(t)>f(0) với mọi t>0 \(\Leftrightarrow t.3^t+1>1\) (4)
kết hợp (3) và (4) ta thấy không thỏa mãn bpt
vậy bpt đã cho tương đương t<0\(\Leftrightarrow log_3\left(x+1\right)< 0\Leftrightarrow x+1< 1\Leftrightarrow x< 0\)
kết hợp ĐK ta có -1<x<0
Ai giải hộ cái bài này với khó quá à
;
;
TT
0
LN
21 tháng 8 2017
tìm 2 điểm A và B . tam giác vuông tại 0 => vecto OA*OB= 0 với O là gốc
LN
21 tháng 8 2017
a đù xem lần đầu sao k có pt h lại có . bài này mk tìm dc denta'=1=> nghiệm x1=m+1:x2=m-1( theo công thức nghiệm)=>A(m+1:0),B(m-1;0) => vì tam giác OAB vuông mà O là gốc nên => tích OA.OB=0 <=>(m+1)*(m-1)+0*0=0 => m^2-1=0 => m=+-1
Q
31 tháng 3 2017
a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
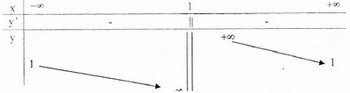
Đồ thị như hình bên.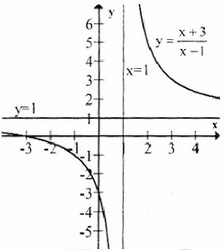 
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
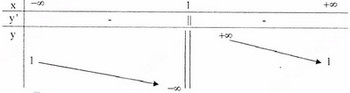
Đồ thị như hình bên.
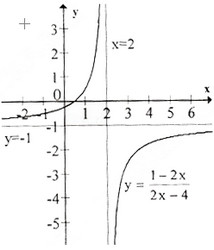
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
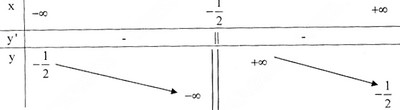
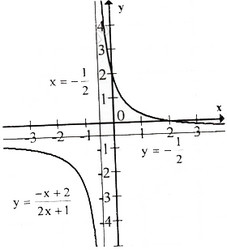
Đồ thị như hình bên.
AH
Akai Haruma
Giáo viên
1 tháng 3 2017
Bài 1)
Gọi số phức $z$ có dạng \(z=a+bi(a,b\in\mathbb{R})\).
Ta có \(|z|+z=3+4i\Leftrightarrow \sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Rightarrow\left\{\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Rightarrow\left\{\begin{matrix}a=\frac{5}{6}\\b=4\end{matrix}\right.\)
Vậy số phức cần tìm là \(\frac{5}{6}+4i\)
b)
\(\left\{\begin{matrix} z_1+3z_1z_2=(-1+i)z_2\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{z_1}{z_2}+3z_1=-1+i\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \frac{z_1}{z_2}+z_1+z_2=(-1+i)-(3+2i)=-4-i\)
\(\Leftrightarrow w=-4-i\Rightarrow |w|=\sqrt{17}\)
khó thật vì ko có kết quả
Sao khó bn,quá dễ :
1 + 1 = 2 .Chứ ví dụ như phép tính : 11+ 11 =
11
+ 11
23