Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

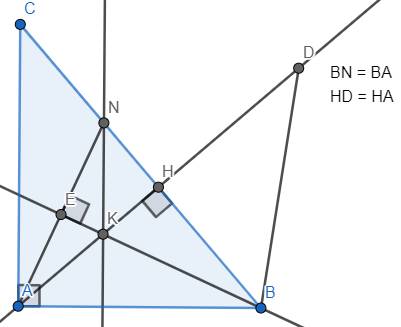
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)

a: Xét ΔBEA vuông tại E và ΔBEN vuông tại E co
BA=BN
BE chung
=>ΔBEA=ΔBEN
b: Xét ΔBAD có
BH vừa là đường cao, vừa là đường trung tuyến
=>ΔBAD cân tại B
c: Xét ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
=>BA=BE
=>ΔBAE cân tại B
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc với BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
nếu bạn không phiền thì có thể vẽ hình ra được không ạ :((

a: Xét ΔBEA vuông tại E và ΔBEN vuông tại Ecó
BE chung
BA=BN
=>ΔBEA=ΔBEN
b: Xet ΔBAD co
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BA=BD
c: Xet ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D co
BE chung
BA=BD
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc B chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B

ĐỀ QUẬN BÌNH TÂN NĂM 2016 - 2017
a) Xét \(\Delta ABH\)và \(\Delta ACH\)ta có:
AH là cạnh chung
AB = AC ( \(\Delta ABC\)cân tại A)
BH = CH ( H là trung điểm của BC)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c-c-c\right)\)
Xét \(\Delta ABC\)cân tại A ta có:
AH là đường trung tuyến ( H là trung điểm của BC)
\(\Rightarrow\)AH là đường cao của \(\Delta ABC\)
\(\Rightarrow AH⊥BC\)tại H.
b) Xét \(\Delta BDH\)vuông tại D và \(\Delta CEH\)vuông tại E ta có:
BH = CH ( H là trung điểm của BC)
\(\widehat{DBH}=\widehat{ECH}\)(\(\Delta ABC\)cân tại A)
\(\Rightarrow\Delta BDH=\Delta CEH\left(ch-gn\right)\)
\(\Rightarrow\)BD = CE ( 2 cạnh tương ứng)
c) Ta có:
AB = AC (\(\Delta ABC\)cân tại A)
BD = CE ( cmt)
\(\Rightarrow AB-BD=AC-CE\)
\(\Rightarrow AD=AE\)
\(\Rightarrow\Delta ADE\)cân tại A
\(\Rightarrow\widehat{ADE}=\frac{180^o-\widehat{DAE}}{2}\)
Mà \(\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\)
Nên \(\widehat{ADE}=\widehat{ABC}\)
Mặt khác 2 góc này nằm ở vị trí đồng vị
\(\Rightarrow\)DE // BC.
d) Nối A với I.
Ta có:
\(\hept{\begin{cases}HE=HM+ME\left(M\in HE\right)\\HM=EN\left(gt\right)\end{cases}}\)
\(\Rightarrow HE=EN+ME\)
\(\Rightarrow HE=MN\)
Xét \(\Delta AEN\)vuông tại E ta có:
\(\hept{\begin{cases}AN^2=AE^2+EN^2\left(Pitago\right)\\AE=AD\left(cmt\right)\\EN=HM\left(gt\right)\end{cases}}\)
\(\Rightarrow AN^2=AD^2+HM^2\)
\(\Rightarrow AN^2=AD^2+HI^2-MI^2\)
\(\Rightarrow AN^2=AD^2+HI^2-\left(NI^2-MN^2\right)\)
\(\Rightarrow AN^2=AD^2+HI^2-NI^2+HD^2\)
\(\Rightarrow AN^2=AD^2+HD^2+HI^2-NI^2\)
\(\Rightarrow AN^2=AH^2+HI^2-NI^2\)
\(\Rightarrow AN^2=AI^2-NI^2\)
\(\Rightarrow AI^2=AN^2+NI^2\)
\(\Rightarrow\Delta ANI\)vuông tại N ( Định lý Pitago đảo)
\(\Rightarrow IN⊥AN\)tại N.

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
=>ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
=>E là trực tâm
=>BE vuông góc KC

Xét ΔBEA vuông tại E và ΔBEN vuông tại E có
BE chung
BA=BN
Do đó: ΔBEA=ΔBEN
Xét ΔBAE vuông tại E và ΔBNE vuông tại E có
. BA=BN (gt)
. BE: cạnh chung
Nên ΔBAE=ΔBNE (ch-cgv)