Question

[Phạm Mai]

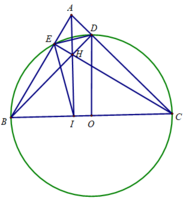
Cho tam giác ABC, đường tròn tâm O đường kính BC cắt AB, AC tại E, D. EC cắt BD tại H. AH cắt BC tại I. Đường thẳng qua I và song song với ED cắt AB tại M và EC tại N. Chứng minh I là trung điểm của MN

Answer 1

[Nguyễn Đình Đạt]

Bước 1: Ta có \(O\) là tâm đường tròn đường kính \(B C\), nên:

• \(\angle B E C = \angle B D C = 90^{\circ}\) → \(E D \bot B C\) tại một số điểm

Bước 2: Gọi \(H = E C \cap B D\), \(A H \cap B C = I\).

Bước 3: Xét phép đối xứng trục qua \(E D\):

• Do \(E D \bot B C\), nên phép đối xứng trục này biến đường thẳng \(A B\) thành \(A C\)
• Biến điểm \(E\) thành \(D\), và ngược lại

Bước 4: Đường qua \(I\), song song \(E D\), cắt \(A B\) tại \(M\), cắt \(E C\) tại \(N\)

→ Do \(I M \parallel E D\), \(I N \parallel E D\) ⇒ Tam giác \(M I N\) là hình thang

Bước 5: Xét các tam giác đồng dạng:

• Do \(\triangle B E C sim \triangle D C B\), và cùng nằm trên đường tròn, ta xét tỉ số đồng dạng và trung tuyến
• Điểm \(I\) là giao điểm của \(A H\) với \(B C\), cũng là giao của 2 đường chéo hình thang MN, vậy để chứng minh \(I\) là trung điểm \(M N\), ta chỉ cần chỉ ra:

\(I M = I N\)

→ Điều này đúng vì \(M N \parallel E D\), mà \(I\) nằm trên đường thẳng chia hai đoạn \(A B , E C\) theo cùng tỷ lệ (do điểm H là giao của EC và BD).

nhớ tick cho mình với nhé

Answer 2

[Nguyễn Đình Đạt]