Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt phóng xạ cần dùng là: \(N=H.\Delta t\)
Vì sau 2 năm, liều lượng phóng xạ dùng như nhau nên:
\(H_0.\Delta t_0=H_1.\Delta t_1\)
\(\Rightarrow \Delta t_1=\dfrac{H_0}{H_1}.\Delta t_0\)
\(H_1=H_0/2^{\dfrac{t}{T}}\)
\(\Rightarrow \Delta t_1=2^\dfrac{t}{T}.\Delta t_0=2^\dfrac{2}{5,27}.10=...\)

Đáp án: D.
Lượng tia γ phóng xạ lần đầu: ΔN1 = N0(1 - e-λDt) » N0λΔt
(áp dụng công thức gần đúng: Khi x << 1 thì 1 - e-x ≈ x, ở đây coi Δt >> T nên
1 - e-λ ∆ t = λ ∆ t)
Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn:
N = N0.2-t/T = N0.2-1/2.
Thời gian chiếu xạ lần này ∆ t’ → ∆ N’ = N0.2-1/2(1 - e - λ ∆ t ' ) » N0.2-1/2 λ ∆ t’
Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ∆ N’ = ∆ N
Do đó ![]() phút.
phút.

- Lượng tia γ phóng xạ lần đầu:
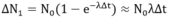
(áp dụng công thức gần đúng: Khi x << 1 thì 1-e-x ≈ x, ở đây coi Δt >> T nên 1 - e-λΔt = λΔt)
- Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn:
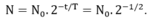
- Thời gian chiếu xạ lần này Δt’:
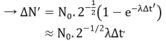
- Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ΔN' = ΔN. Do đó:
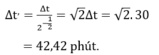

Lượng tia γ phóng xạ lần đầu: ∆N1 = N0(1-e-λ∆t) ≈ N0λ∆t
(áp dụng công thức gần đúng: Khi x << 1 thì 1-e-x » x, ở đây coi ∆t >> T nên 1 - e-λDt = λDt)
Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn: N1 = N0.2-t/T = N0.2-1/2
Thời gian chiếu xạ lần này Dt’ → ∆N’ = C(1-e-λ∆t’) ≈ N0.2-1/2λ∆t’
Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ∆N’ = ∆N
Do đó ∆t’= ∆t/2-1/2 = √2∆t = √2.30 = 42,42 phút.
Chọn đáp án D

khi x rất nhỏ có: e - x = 1 - x
Xem lượng tia gamma phát ra tỉ lệ với số nguyên tử bị phân rã.
Số nguyên tử bị phân trong lần chiếu xạ đầu tiên:
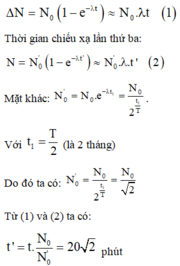
Đáp án C

Trong điều trị ung thư, bệnh nhân được uống hoặc tiêm thuốc hóa trị (hóa chất chống ung thư) để tiêu diệt hoặc ức chế sự phát triển của tế bào ung thư."
thuốc hóa trị