
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tam giác MQE vuông tại E \(\Rightarrow\widehat{EMQ}+\widehat{EQM}=90^0\) (1)
Mà \(\widehat{EQM}\) là góc ngoài của tam giác NPQ, theo tính chất góc ngoài của tam giác:
\(\widehat{EQM}=\widehat{ENP}+\widehat{QPN}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}=90^0\)
\(\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}-90^0=0\)

Bạn làm ơn chụp ảnh rõ hơn được không? Mình không nhìn thấy gì hết ớ!

\(B=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right).\left(\frac{1}{4^2}-1\right)......\left(\frac{1}{100^2}-1\right).\)
\(B=\frac{-3}{2^2}\times\frac{-8}{3^2}\times\frac{-15}{4^2}\times.....\times\frac{-9999}{100^2}\)
\(B=-\left(\frac{3}{2^2}\times\frac{8}{3^2}\times.....\times\frac{9999}{100^2}\right)\)(vì A là tích của 99 thừa số âm nên kết quả là âm )
\(B=-\left(\frac{1.3}{2.2}\times\frac{2.4}{3.3}\times.....\times\frac{99.101}{100.100}\right)\)
\(B=-\left(\frac{1.2.3...99}{2.3.4.....100}\times\frac{3.4.5....101}{2.3.4....100}\right)\)
\(B=-\left(\frac{1}{100}\times\frac{101}{2}\right)\)
\(B=-\frac{101}{200}\)

b) Vì \(\hept{\begin{cases}2a=3b\\4b=5c\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{3}=\frac{b}{2}\\\frac{b}{5}=\frac{c}{4}\end{cases}}\) \(\Rightarrow\hept{\begin{cases}\frac{a}{15}=\frac{b}{10}\\\frac{b}{10}=\frac{c}{8}\end{cases}}\Rightarrow\frac{a}{15}=\frac{b}{10}=\frac{c}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{15}=\frac{b}{10}=\frac{c}{8}=\frac{2a}{30}=\frac{2c}{16}=\frac{2a-b-2c}{30-10-16}=\frac{4}{4}=1\)
\(\Rightarrow\hept{\begin{cases}a=15\\b=10\\c=8\end{cases}}\)
Câu 5 :
Vì \(\hept{\begin{cases}a=2b\\b=3c\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a}{2}=\frac{b}{1}\\\frac{b}{3}=\frac{c}{1}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=\frac{b}{3}\\\frac{b}{3}=\frac{c}{1}\end{cases}}\Rightarrow\frac{a}{6}=\frac{b}{3}=\frac{c}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{6}=\frac{b}{3}=\frac{c}{1}=\frac{2b}{6}=\frac{3c}{3}=\frac{a-2b+3c}{6-6+3}=\frac{6}{3}=2\)
\(\Rightarrow\hept{\begin{cases}a=2.6=12\\b=2.3=6\\c=2.1=2\end{cases}}\)

Bài 1 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{12}=\frac{y}{-8}=\frac{x+y}{12+\left(-8\right)}=\frac{-48}{4}=-12.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=-12\\\frac{y}{-8}=-12\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-144\\y=96\end{cases}}\)
b ) Từ \(x\):\(\left(-7\right)\)= \(y\): \(10\)
\(\Rightarrow\)\(\frac{x}{-7}=\frac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-7}=\frac{y}{10}=\frac{y-x}{10-\left(-7\right)}=\frac{-34}{17}=-2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-7}=-2\\\frac{y}{10}=-2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=14\\y=-20\end{cases}}\)
c ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{-12}=\frac{2x}{30}=\frac{y}{-12}=\frac{2x+y}{30+\left(-12\right)}=\frac{-360}{18}=-20\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=-20\\\frac{y}{-12}=-20\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-300\\y=240\end{cases}}\)
d ) Từ \(2x=-3y\)\(\Rightarrow\)\(\frac{x}{-3}=\frac{y}{2}\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{-3}=\frac{y}{2}=\frac{x}{-3}=\frac{5y}{10}=\frac{x-5y}{-3-10}=\frac{-130}{-13}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=10\\\frac{y}{2}=10\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-30\\y=20\end{cases}}\)
Bài 2 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=\frac{x+y-z}{2+\left(-3\right)-5}=\frac{-54}{-6}=9.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=9\\\frac{y}{-3}=9\\\frac{z}{5}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=18\\y=-27\\z=45\end{cases}}\)
b ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{-7}=\frac{z}{3}=\frac{x}{4}=\frac{2y}{-14}=\frac{z}{3}=\frac{x+2y-z}{4+\left(-14\right)-3}=\frac{-39}{-13}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=3\\\frac{y}{-7}=3\\\frac{z}{3}=3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=12\\y=-21\\z=9\end{cases}}\)


Bài 4
a/ \(x=\widehat{ABC};y=\widehat{ADC}\)
Ta có a//b; \(a\perp c\Rightarrow b\perp c\Rightarrow x=\widehat{ABC}=90^o\)
Xét tứ giác ABCD
\(y=\widehat{ADC}=360^o-\widehat{BAD}-\widehat{ABC}-\widehat{BCD}\) (tổng các góc trong của tứ giác = 360 độ)
\(\Rightarrow y=\widehat{ADC}=360^o-90^o-90^o-130^o=50^o\)
b/ Kéo dài n về phí B cắt AC tại D
\(\Rightarrow\widehat{CBD}=180^o-\widehat{nBC}=180^o-105^o=75^o\)
Xét tg BCD có
\(\widehat{BDC}=180^o-\widehat{CBD}-\widehat{BCD}=180^o-75^o-60^o=45^o=\widehat{mAC}\)
=> Am//Bn (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành hai góc đồng vị bằng nhau thì chúng // với nhau)
Bài 5
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3a}=\frac{a+b+c}{3\left(a+b+c\right)}=\frac{1}{3}\)
Ta có \(\frac{a}{3b}=\frac{b}{3c}=\frac{a+b}{3\left(b+c\right)}=\frac{1}{3}\Rightarrow\frac{a+b}{b+c}=1\Rightarrow a+b=b+c\)
\(\frac{b}{3c}=\frac{c}{3a}=\frac{b+c}{3\left(c+a\right)}=\frac{1}{3}\Rightarrow\frac{b+c}{c+a}=1\Rightarrow b+c=c+a\)
\(\Rightarrow a+b=b+c=c+a\)
\(\frac{c}{3a}=\frac{a}{3b}=\frac{c+a}{3\left(a+b\right)}=\frac{1}{3}\Rightarrow\frac{c+a}{a+b}=1\)
Từ \(\frac{a+b}{b+c}=\frac{a}{b+c}+\frac{b}{b+c}=\frac{a}{b+c}+\frac{b}{c+a}=1\) (1)
Từ \(\frac{b+c}{c+a}=\frac{b}{c+a}+\frac{c}{c+a}=\frac{b}{c+a}+\frac{c}{a+b}=1\) (2)
Từ \(\frac{c+a}{a+b}=\frac{c}{a+b}+\frac{a}{a+b}=\frac{c}{a+b}+\frac{a}{b+c}=1\) (3)
Công 2 vế của (1) (2) và (3)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{c}{a+b}+\frac{a}{b+c}=3\)
\(\Rightarrow2\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=3.\)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=\frac{3}{2}\)
\(\Rightarrow M=2018\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=\frac{2018.3}{2}=3027\)

ta có : Do NB song song với MA nên
\(\hept{\begin{cases}\widehat{ABN}+\widehat{MAB}=180^0\\\widehat{ABN}-\widehat{MAB}=40^0\end{cases}}\Rightarrow2\widehat{MAB}=180^0-40^0=140^0\)
Nên \(\widehat{MAB}=70^0\)


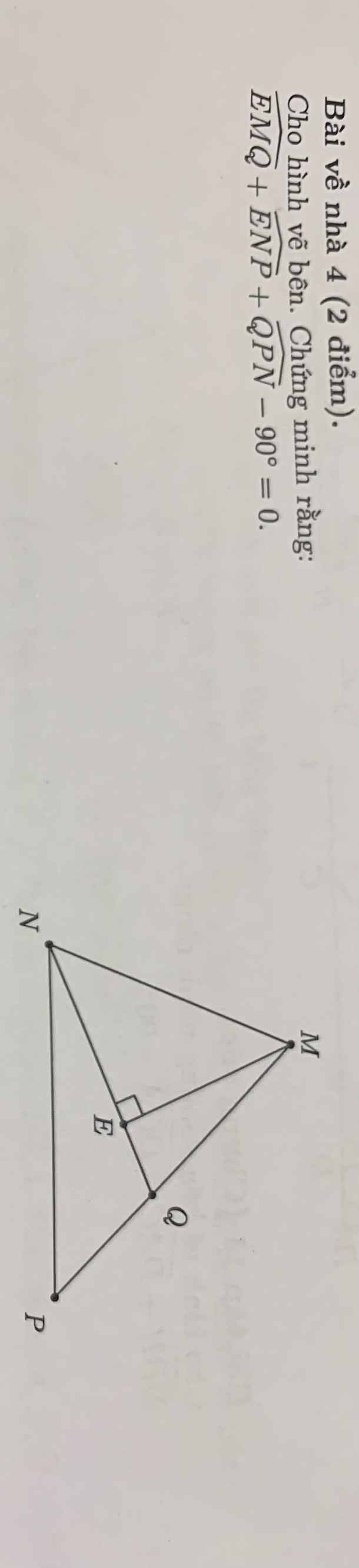
 Bài 56
Bài 56 bài 38,39,40
bài 38,39,40 Bài 42->46
Bài 42->46 Mọi người làm giúp e nhá !! Giải chi tiết rõ ràng, ko thấy inb hỏi e ạ
Mọi người làm giúp e nhá !! Giải chi tiết rõ ràng, ko thấy inb hỏi e ạ  lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều!
lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều!

 Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;
Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;

 Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Chào bạn, để giải quyết các bài toán này, mình sẽ trình bày từng bước như sau:
Câu 14:
a) Tìm Q(x) = A(x) - B(x)?
Để tìm Q(x), bạn cần cung cấp đa thức A(x) và B(x). Khi đó, bạn chỉ cần thực hiện phép trừ tương ứng giữa các hệ số của các số hạng đồng bậc.
Ví dụ: Nếu A(x) = \(3 x^{2} + 2 x - 1\) và B(x) = \(x^{2} - x + 2\), thì:
\(Q \left(\right. x \left.\right) = \left(\right. 3 x^{2} + 2 x - 1 \left.\right) - \left(\right. x^{2} - x + 2 \left.\right) = 2 x^{2} + 3 x - 3\)b) (TLS) Tính B(x).C(x)? Chứng tỏ x = -1 là nghiệm của đa thức C(x)
Tương tự, bạn cần cung cấp đa thức B(x) và C(x). Sau khi có, bạn thực hiện phép nhân đa thức.
Ví dụ: Nếu B(x) = \(x + 1\) và C(x) = \(x - 2\), thì:
\(B \left(\right. x \left.\right) \cdot C \left(\right. x \left.\right) = \left(\right. x + 1 \left.\right) \left(\right. x - 2 \left.\right) = x^{2} - x - 2\)Để chứng tỏ x = -1 là nghiệm của đa thức C(x), bạn thay x = -1 vào C(x) và kiểm tra xem kết quả có bằng 0 không.
Ví dụ: Nếu C(x) = \(x + 1\), thì C(-1) = -1 + 1 = 0. Vậy x = -1 là nghiệm của C(x).
Câu 15:
(TL2) Đội múa có 1 bạn nam và 5 bạn nữ, Chọn ngẫu nhiên 1 bạn để phỏng vấn. Tính xác suất của biến cố bạn được chọn là nam.
Tổng số bạn trong đội múa là 1 + 5 = 6 bạn.
Xác suất chọn được bạn nam là số bạn nam chia cho tổng số bạn:
\(P \left(\right. \text{ch}ọ\text{n}\&\text{nbsp};\text{nam} \left.\right) = \frac{1}{6}\)Câu 16:
(3.25đ) Cho tam giác ABC vuông tại A có B = 60°. Trên BC lấy điểm H sao cho HB = BA, từ H kẻ HE vuông góc với BC tạ H, (E thuộc AC)
a) (TL3) Tính C
Trong tam giác ABC vuông tại A, ta có:
\(\angle B + \angle C = 90^{\circ}\) \(\angle C = 90^{\circ} - \angle B = 90^{\circ} - 60^{\circ} = 30^{\circ}\)b) (TL4) Chứng minh BE là tia phân giác góc B
Vì tam giác ABH có AB = BH, nên tam giác ABH cân tại B. Do đó:
\(\angle B A H = \angle B H A\)Mà HE vuông góc với BC tại H, nên:
\(\angle B H A + \angle A H E = 180^{\circ}\)(Bạn cần cung cấp thêm thông tin hoặc hình vẽ để chứng minh BE là tia phân giác góc B một cách đầy đủ).
c) (TL5) Gọi K là giao điểm của BA và HE. CMR: BE vuông góc với KC
(Cần thêm thông tin hoặc hình vẽ để chứng minh)
d) (TL9) Khi tam giác ABC có BC = 2AB. Tính B
Nếu BC = 2AB, thì sin(C) = AB/BC = 1/2. Vậy góc C = 30 độ và góc B = 60 độ.
Câu 17 (thêm):
Cho ∆ABC vuông tại A (AB < AC), BK là tia phân giác của góc ABC (K∈ AC). Kẻ KI vuông góc với BC tại I.
a) Chứng minh: ΔΑΒΚ = ΔΙΒΚ.
Xét hai tam giác vuông ΔΑΒΚ và ΔΙΒΚ có:
Vậy ΔΑΒΚ = ΔΙΒΚ (cạnh huyền - góc nhọn).
b) Kẻ AD vuông góc với BC. Chứng minh: AI là tia phân giác của góc DAK.
(Cần thêm thông tin hoặc hình vẽ để chứng minh)
c) Gọi H là giao điểm của BK và AD. Chứng minh: HB + IC < AB + AC.
(Cần thêm thông tin hoặc hình vẽ để chứng minh)
Để giải quyết các phần còn thiếu, bạn vui lòng cung cấp thêm thông tin hoặc hình vẽ nhé!