Question

[Hiền Phan]

Cho tam giác ABC nhọn ( AB < AC), đường tròn (O) đường kính BC cắt AB , AC lần lượt tại E và D . CE cắt BD tại H .
a) Chứng minh: tứ giác BEDC là tứ giác nội tiếp
b) Gọi F là giao điểm của AH và BC . Chứng minh : FA là tia phân giác của DFE .
c) Cho biết BCD = 45 độ ; BCE = 15 độ và BC = 4m . Tính diện tích tứ giác BEDC

Answer 1

[An Phan]

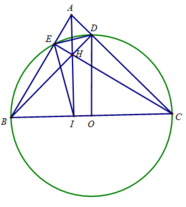
Giả thiết:

• Tam giác ABC nhọn, AB < AC.
• (O) là đường tròn đường kính BC.
• Đường tròn (O) cắt AB tại E, cắt AC tại D.
• Đường thẳng CE cắt BD tại H.
• F là giao điểm của AH và BC.

---

a) Chứng minh tứ giác BEDC là tứ giác nội tiếp

Ta cần chứng minh 4 điểm B, E, D, C cùng nằm trên 1 đường tròn.

Ta biết (O) là đường tròn đường kính BC, nên mọi điểm nằm trên đường tròn và nối với B và C sẽ tạo góc vuông.

• Vì E nằm trên đường tròn và thuộc đoạn AB, nên:
  \(\angle B E C = 90^{\circ}\)
• Tương tự, D thuộc AC và nằm trên đường tròn, nên:
  \(\angle B D C = 90^{\circ}\)

Mà hai góc này là góc nội tiếp chắn cung đối nhau, nên:

• \(\angle B E C + \angle B D C = 180^{\circ}\)

⇒ Tứ giác BEDC có tổng hai góc đối là \(180^{\circ}\), nên BEDC là tứ giác nội tiếp.

✅ Đpcm

---

b) Chứng minh FA là tia phân giác của góc DFE

Phân tích:

• Từ phần a), tứ giác BEDC nội tiếp.
• Giao điểm H của CE và BD có thể xem là giao điểm hai đường chéo của tứ giác nội tiếp.

=> Dựa vào định lý tứ giác nội tiếp có hai đường chéo cắt nhau tại H thì tia AH là tia phân giác của góc DFE, ta có:

• AH là tia phân giác của góc DFE
  → Giao điểm F của AH và BC nằm trên phân giác của góc DFE.

✅ Đpcm

---

c) Cho biết:

• \(\angle B C D = 45^{\circ}\)
• \(\angle B C E = 15^{\circ}\)
• \(B C = 4 \textrm{ } m\)

Tính diện tích tứ giác BEDC

Tứ giác BEDC gồm hai tam giác:

• Tam giác BDC
• Tam giác BEC

1. Tính diện tích tam giác BDC

Sử dụng công thức:

\(S = \frac{1}{2} \cdot B C^{2} \cdot sin ⁡ \left(\right. \angle B C D \left.\right)\)

Vì D và C cùng nằm trên đường tròn (O), tam giác BDC vuông tại D ⇒ \(\angle B D C = 90^{\circ}\), nên:

\(S_{B D C} = \frac{1}{2} \cdot B C^{2} \cdot sin ⁡ \left(\right. \angle B C D \left.\right) = \frac{1}{2} \cdot 4^{2} \cdot sin ⁡ \left(\right. 45^{\circ} \left.\right) = \frac{1}{2} \cdot 16 \cdot \frac{\sqrt{2}}{2} = 8 \cdot \frac{\sqrt{2}}{2} = 4 \sqrt{2} \textrm{ } \left(\right. m^{2} \left.\right)\)

---

2. Tính diện tích tam giác BEC

Góc \(\angle B E C = 90^{\circ}\) (vì nằm trên đường tròn đường kính BC)

Tương tự:

\(S_{B E C} = \frac{1}{2} \cdot B C^{2} \cdot sin ⁡ \left(\right. \angle B C E \left.\right) = \frac{1}{2} \cdot 4^{2} \cdot sin ⁡ \left(\right. 15^{\circ} \left.\right) = 8 \cdot sin ⁡ \left(\right. 15^{\circ} \left.\right)\)

Mà:
\(sin ⁡ \left(\right. 15^{\circ} \left.\right) = sin ⁡ \left(\right. 45^{\circ} - 30^{\circ} \left.\right) = \frac{\sqrt{6} - \sqrt{2}}{4}\)

→

\(S_{B E C} = 8 \cdot \frac{\sqrt{6} - \sqrt{2}}{4} = 2 \cdot \left(\right. \sqrt{6} - \sqrt{2} \left.\right)\)

---

Tổng diện tích tứ giác BEDC:

\(S = S_{B D C} + S_{B E C} = 4 \sqrt{2} + 2 \left(\right. \sqrt{6} - \sqrt{2} \left.\right) = 4 \sqrt{2} + 2 \sqrt{6} - 2 \sqrt{2} = 2 \sqrt{2} + 2 \sqrt{6} = 2 \left(\right. \sqrt{2} + \sqrt{6} \left.\right) \textrm{ } \left(\right. m^{2} \left.\right)\)

✅ Đáp án: \(\boxed{2 \left(\right. \sqrt{2} + \sqrt{6} \left.\right) \textrm{ } m^{2}}\)

Answer 2

[Nguyễn Lê Phước Thịnh]

a: Vì B,E,D,C cùng thuộc (O)

nên BEDC là tứ giác nội tiếp

b: Xét (O) có

ΔBDC nội tiếp

BC là đường kính

Do đó: ΔBDC vuông tại D

=>BD⊥AC tại D

Xét (O) có

ΔCEB nội tiếp

CB là đường kính

Do đó: ΔCEB vuông tại E

=>CE⊥AB tại E

Xét ΔABC có

BD,CE là các đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH⊥BC tại F

Xét tứ giác CDHF có \(\hat{CDH}+\hat{CFH}=90^0+90^0=180^0\)

nên CDHF là tứ giác nội tiếp

Xét tứ giác BEHF có \(\hat{BEH}+\hat{BFH}=90^0+90^0=180^0\)

nên BEHF là tứ giác nội tiếp

Ta có: \(\hat{DFH}=\hat{DCH}\) (CDHF nội tiếp)

\(\hat{EFH}=\hat{EBH}\) (BEHF nội tiếp)

mà \(\hat{DCH}=\hat{EBH}\left(=90^0-\hat{BAC}\right)\)

nên \(\hat{DFH}=\hat{EFH}\)

=>FA là phân giác của góc DFE