Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Fe_______________________Fe2+
Fe3O4______NaHSO4 0,32 \(\rightarrow\)Fe3+_______+NO 0,04 +H2O
Fe(NO3)2 ________________Na+ 0,32
_________________________SO42- 0,32
_________________________NO3-
_________________________53,92g
Theo bảo toàn H: nNaHSO4=2nH2O=0,32
\(\rightarrow\)nH2O=0,16
Theo bảo toàn khối lượng
m+mNaHSO4=m muối+mNO+mH2O
\(\rightarrow\)m+0,32.120=53,92+0,04.30+0,16.18
\(\rightarrow\)m=19,6

A: `N_2`
C: `NO`
D: `NO_2`
E: `HNO_3`
G: `NaNO_3`
\(\left(1\right)2NH_3+3CuO\underrightarrow{t^o}3Cu+N_2+3H_2O\)
\(\left(2\right)N_2+3H_2\underrightarrow{xt,t^o}2NH_3\)
\(\left(3\right)4NH_3+5O_2\underrightarrow{xt,t^o}6H_2O+4NO\)
\(\left(4\right)2NO+O_2\rightarrow2NO_2\)
\(\left(5\right)4NO_2+O_2+2H_2O\rightarrow4HNO_3\)
\(\left(6\right)HNO_3+NaOH\rightarrow NaNO_3+H_2O\)

Vì A và B là hiđrocacbon nên khi đốt cháy chỉ thu được CO2 và H2O.
Ta có: \(n_{O_2}=\dfrac{64}{32}=2\left(mol\right)\)
\(n_{CO_2}=n_{CaCO_3}=\dfrac{100}{100}=1\left(mol\right)\)
Khí ra khỏi bình là O2 dư.
\(\Rightarrow n_{O_2\left(dư\right)}=\dfrac{pV}{RT}=\dfrac{0,4.11,2}{0,082.273}=0,2\left(mol\right)\)
BTNT O, có: \(n_{H_2O}=2n_{O_2}-2n_{O_2\left(dư\right)}-2n_{CO_2}=1,6\left(mol\right)\)
Có: nH2O > nCO2 nên A và b là ankan.
⇒ nankan = nH2O - nCO2 = 0,6 (mol)
Giả sử CTPT chung của A và B là: \(C_{\overline{n}}H_{2\overline{n}+2}\).
Có: n = số nguyên tử C = \(\dfrac{1}{0,6}=1,67\)
Mà: A và B là 2 ankan kế tiếp.
Nên A và B lần lượt là CH4 và C2H6.
Bạn tham khảo nhé!

1. Công thức electron, công thức Lewis và công thức cấu tạo của phân tử nitrogen lần lượt là:
\(:N:::N:\\ :N\equiv N:\\ N\equiv N\)
2.
\(E_b\left(N_2\right)\) lớn vì giữa hai nguyên tử N có liên kết ba bền.
Do đó, nitrogen khá trơ ở điều kiện thường.
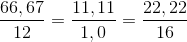 = 4 :8 : 1
= 4 :8 : 1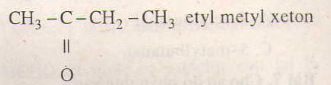
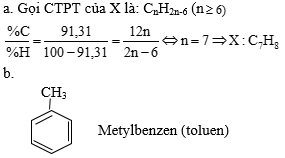
Cho
\(y = \frac{2 x}{x + 2} , M \left(\right. x_{0} , y_{0} \left.\right) \textrm{ }\textrm{ } \left(\right. x_{0} > 0 \left.\right) , y_{0} = \frac{2 x_{0}}{x_{0} + 2} .\)
Ta có
\(y^{'} = \frac{\left(\right. x + 2 \left.\right) \cdot 2 - 2 x \cdot 1}{\left(\right. x + 2 \left.\right)^{2}} = \frac{4}{\left(\right. x + 2 \left.\right)^{2}}\)
nên tại \(x = x_{0}\), hệ số góc tiếp tuyến là
\(m = \frac{4}{\left(\right. x_{0} + 2 \left.\right)^{2}} .\)
Phương trình tiếp tuyến ở \(M\) là
\(y - y_{0} = m \textrm{ } \left(\right. x - x_{0} \left.\right) \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y = \textrm{ }\textrm{ } m \textrm{ } x + \underset{b}{\underbrace{\left(\right. y_{0} - m \textrm{ } x_{0} \left.\right)}} .\)
\(b = y_{0} - m x_{0} = \frac{2 x_{0}}{x_{0} + 2} \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \frac{4}{\left(\right. x_{0} + 2 \left.\right)^{2}} \textrm{ } x_{0} = \frac{2 x_{0}^{2}}{\left(\right. x_{0} + 2 \left.\right)^{2}} .\)
\(x_{A} = - \frac{b}{m} = - \frac{2 x_{0}^{2} / \left(\right. x_{0} + 2 \left.\right)^{2}}{4 / \left(\right. x_{0} + 2 \left.\right)^{2}} = - \frac{2 x_{0}^{2}}{4} = x_{0} \left(\right. 1 - \frac{x_{0}}{2} \left.\right) .\)
\(y_{B} = b = \frac{2 x_{0}^{2}}{\left(\right. x_{0} + 2 \left.\right)^{2}} .\)
Diện tích tam giác \(\left(\right. 0 , 0 \left.\right) , \left(\right. x_{A} , 0 \left.\right) , \left(\right. 0 , y_{B} \left.\right)\) là
\(\frac{x_{A} \textrm{ } y_{B}}{2} = \frac{1}{2} \textrm{ } \left[\right. x_{0} \left(\right. 1 - \frac{x_{0}}{2} \left.\right) \left]\right. \textrm{ } \frac{2 x_{0}^{2}}{\left(\right. x_{0} + 2 \left.\right)^{2}} = \frac{x_{0}^{3} \left(\right. 1 - \frac{x_{0}}{2} \left.\right)}{\left(\right. x_{0} + 2 \left.\right)^{2}} .\)
Theo giả thiết,
\(\frac{x_{0}^{3} \left(\right. 1 - \frac{x_{0}}{2} \left.\right)}{\left(\right. x_{0} + 2 \left.\right)^{2}} = \frac{1}{18} .\)
Giải phương trình này (nhẩm hoặc dùng phép hoá đơn giản) ta tìm được
\(x_{0} = 1 (\text{v} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{m}ộ\text{t}\&\text{nbsp};\text{nghi}ệ\text{m}\&\text{nbsp};\text{th}ứ\&\text{nbsp};\text{hai}\&\text{nbsp};\text{x} \overset{ˊ}{\hat{\text{a}}} \text{p}\&\text{nbsp};\text{x}ỉ\&\text{nbsp}; 1,686 \&\text{nbsp};\text{nh}ư\text{ng}\&\text{nbsp};\text{kh} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{cho}\&\text{nbsp};\text{k} \overset{ˊ}{\hat{\text{e}}} \text{t}\&\text{nbsp};\text{qu}ả\&\text{nbsp};\text{nguy} \hat{\text{e}} \text{n}/\text{h}ữ\text{u}\&\text{nbsp};\text{t}ỉ\&\text{nbsp};đẹ\text{p}) .\)
Với \(x_{0} = 1\) ta có
\(y_{0} = \frac{2 \cdot 1}{1 + 2} = \frac{2}{3} ,\) \(P = x_{0} + y_{0} = 1 + \frac{2}{3} = \frac{5}{3} .\)
Đáp số câu 1: \(P = \frac{5}{3} .\)