Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


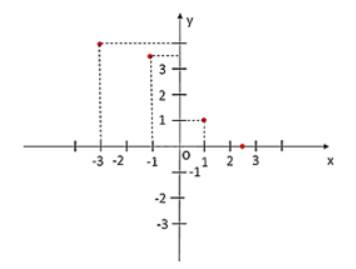
a có tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 3; 4); (– 1; 3,5); (1; 1); (2,5; 0)}.
Biểu diễn các điểm trên lên mặt phẳng tọa độ Oxy ta được đồ thị của hàm số y = f(x).

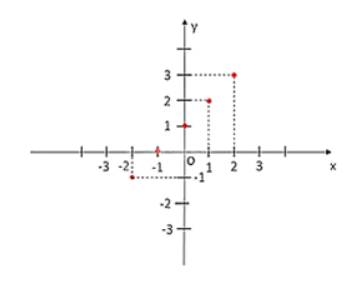
a) Tập hợp các cặp giá trị tương ứng của x và y là:
{(–2; –1); (–1; 0); (0; 1); (1; 2); (2; 3)}.
b) Ta biểu diễn các điểm đã cho như sau:

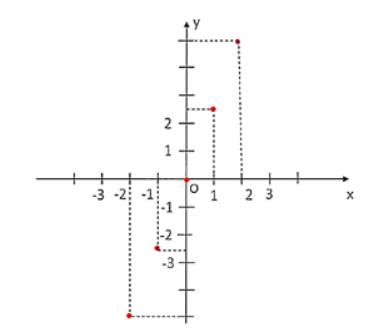
Tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 2; – 5); (– 1; – 2,5); (0; 0); (1; 2,5); (2; 5)}.
Biểu diễn các điểm trên trên cùng một mặt phẳng tọa độ ta được đồ thị hàm số y = f(x) như sau:

a) Nhiệt độ của Hà Nội vào 12h trưa là 30 °C
b) Với mỗi giá trị của t, ta xác định được 1 giá trị tương ứng của T

a) \(y=ax+3\)
Khi \(x=1;y=5\)
\(\Rightarrow5=a.1+3\)
\(\Rightarrow a=2\)
\(\Rightarrow y=2x+3\)
b) \(x=-2\Rightarrow y=-1\)
\(x=-1\Rightarrow y=1\)
\(x=0\Rightarrow y=3\)
\(x=1\Rightarrow y=5\)
\(x=2\Rightarrow y=7\)
1: Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔAHD~ΔBAD
2: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó: ΔAHB~ΔBCD
3: ΔAHB~ΔBCD
=>\(\dfrac{AH}{BC}=\dfrac{HB}{CD}\)
=>\(\dfrac{AH}{HB}=\dfrac{BC}{CD}\)
=>\(AH\cdot CD=BH\cdot BC\)
4: Xét ΔBCD có CE là phân giác
nên \(\dfrac{BE}{ED}=\dfrac{BC}{CD}\)
mà \(\dfrac{BC}{CD}=\dfrac{AH}{HB}\)
nên \(\dfrac{AH}{HB}=\dfrac{BE}{ED}\)
=>\(AH\cdot ED=BE\cdot BH\)
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Lấy điểm E trên DH và điểm K trên BC sao cho DEDH=CKCBDEDH=CKCB. Chứng minh:
a) ΔADE∽ΔACK;ΔADE∽ΔACK;
b) ΔAEK∽ΔADC;ΔAEK∽ΔADC;
c) ˆAEK=900AEK^=900