Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

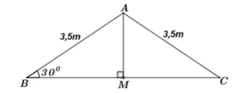
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: ∆ ABC cân tại A
![]()
Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.
Gọi M là trung điểm của BC.
=> AM là đường trung tuyến đồng thời là đường cao của ABC (tính chất).
Xét ∆ ABM vuông tại M ta có:
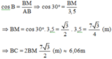
Vậy bề rộng mái nhà là 6,06m
Đáp án cần chọn là: B

Một cửa quay bao gồm 3 cánh cửa có khả năng quay trong một căn phòng hình tròn. Đường kính của căn phòng này là 2 mét (200cm). 3 cánh cửa chia căn phòng ra làm 3 phần có diện tích bằng nhau. Sau đây là sơ đồ cánh cửa tại các vị trí khác nhau, khi nhìn từ góc thẳng đứng phía trên:
2 phần cửa ra vào (phần nét đứt) có kích thước bằng nhau. Nếu phần cửa ra và cửa vào có kích cỡ quá lớn, các cánh cửa sẽ không thể ngăn cách không gian; một luồng không khí có thể đi thẳng qua 2 cánh cửa, từ bên ngoài tòa nhà vào bên trong tòa nhà (gây tăng/giảm nhiệt độ trong nhà một cách không mong muốn). Nhìn hình dưới đây để hình dung ra đường đi của luồng không khí trong trường hợp kích cỡ của 2 cánh cửa quá lớn.
Vậy, chiều dài tối đa của đường cong nét đứt của mỗi phần cửa ra/vào là gì, để không khí không thể đi thẳng từ cửa ra tới cửa vào và ngược lại?
Câu trả lời
Điểm tối đa: Câu trả lời là từ 103 tới 105. Câu trả lời được chấp nhận được tính bởi công thức bằng 1/6 của chu vi hình tròn bao quanh căn phòng. Câu trả lời bằng 100 cũng được chấp nhận, nếu thí sinh tính pi = 3. Nếu trả lời là 100 và không đưa ra giải thích như trên, câu trả lời sẽ không được tính điểm (bởi thí sinh có thể đã đoán câu trả lời bằng với chiều dài của cánh cửa, tức là bán kính của hình tròn).
Không tính điểm: Tất cả các câu trả lời khác. Không tính câu trả lời 209 (tương đương với tổng kích cỡ của cả 2 cửa, thay vì mỗi cửa như yêu cầu đề bài).

1) Bằng kiến thức của bạn về đường tròn, hãy giải thích tại sao bánh xe lại luôn có dạng hình tròn và không bao giờ có dạng khác?
vì khi lăn, thì trọng tâm hình tròn không thay đổi độ cao, còn các hình khác thì luôn thay đổi độ cao, do đó bánh xe hình tròn thì đi sẽ không bị sóc.
2) Tại sao các cốc, chai, chậu,... lại thường có đáy là hình tròn mà có rất ít cốc, chai, chậu,... có đáy hình vuông hay tam giác ...?
vì đáy hình tròn là chậu có thể tích lớn nhất trong các loại chậu cùng chiều cao.
3) Một số nhà hát được xây theo dạng hình tròn (gọi là nhà hát vòng tròn) dựa vào tính chất gì của đường tròn?
nhà hát xây theo hình elip chứ không phải hình tròn, nhưng có lẽ ý bạn là tính chất nhìn một cung cho trước 1 góc không đổi.
4) Nhà của 4 bạn An, Bình, Cường, Dũng đều nằm ở trên biên của một khoảnh đất hình tròn theo đúng thứ tự đó. Biết khoảng cách từ nhà An đến nhà Bình là 3km, từ nhà Bình đến nhà Cường là 4km, từ nhà Cường đến nhà Dũng là 5km, từ nhà Dũng đến nhà An là 6km và từ nhà An đến nhà Cường là 13km. Tính khoảng cách từ nhà Bình đến nhà Dũng.

ta có thể thấy khoảng cách An- Bình (AB) Bình - Cường (BC) và An- Cường (AC) là mâu thuẫn với bất đẳng thức tam giác thế nên đề bài này sai nhé

a) Bài toán: “Nhà kính mái vòm dạng parabol, đỉnh cao 4 m, hai chân cách nhau 4 m. Tìm kích thước cửa chữ nhật lớn nhất đặt dưới mái vòm.”
Phân tích & giải
\(y = a x^{2} + 4.\)
Khi \(x = 2\) hoặc \(x = - 2\), \(y = 0\). Thay \(x = 2 , \textrm{ } y = 0\) → \(0 = a \cdot 2^{2} + 4 \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } 4 a + 4 = 0 \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } a = - 1.\)
\(y = - \textrm{ } x^{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 4.\)
\(H = - \textrm{ } x^{2} + 4.\)
\(A \left(\right. x \left.\right) = \left(\right. \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{r}ộ\text{ng} \left.\right) \times \left(\right. \text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{cao} \left.\right) = \left(\right. 2 x \left.\right) \textrm{ } \left(\right. - x^{2} + 4 \left.\right) = 2 x \textrm{ } \left(\right. - x^{2} + 4 \left.\right) = - 2 x^{3} + 8 x .\)
\(A^{'} \left(\right. x \left.\right) = \frac{d}{d x} \left(\right. - 2 x^{3} + 8 x \left.\right) = - 6 x^{2} + 8.\)
\(- 6 x^{2} + 8 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } 6 x^{2} = 8 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x^{2} = \frac{8}{6} = \frac{4}{3} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x = \sqrt{\frac{4}{3}} = \frac{2}{\sqrt{3}} \left(\right. \text{ch}ỉ\&\text{nbsp};\text{l} \overset{ˊ}{\hat{\text{a}}} \text{y}\&\text{nbsp}; x > 0 \left.\right) .\)
\(H = - \textrm{ } x^{2} + 4 = - \left(\right. \frac{4}{3} \left.\right) + 4 = 4 - \frac{4}{3} = \frac{12 - 4}{3} = \frac{8}{3} \&\text{nbsp};\text{m} .\)
\(\boxed{\text{Chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{r}ộ\text{ng}\&\text{nbsp}; = \frac{4}{\sqrt{3}} \&\text{nbsp};\text{m} , \text{Chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{cao}\&\text{nbsp}; = \frac{8}{3} \&\text{nbsp};\text{m} .}\)
b) Bài toán: “Ống thép mạ kẽm dài ống hồi l = …, đường kính ngoài 6 cm, độ dày ống là 3 mm. Tính thể tích phần thép (tức lớp thép)?”
\(V_{\text{ngo} \overset{ˋ}{\text{a}} \text{i}} = \pi \textrm{ } R_{\text{ngo} \overset{ˋ}{\text{a}} \text{i}}^{2} \times l = \pi \cdot 3^{2} \cdot l = 9 \pi \textrm{ } l \left(\right. \text{cm}^{3} \left.\right) .\)
\(V_{\text{trong}} = \pi \textrm{ } R_{\text{trong}}^{2} \times l = \pi \cdot \left(\right. 2,7 \left.\right)^{2} \cdot l = \pi \cdot 7,29 \cdot l = 7,29 \textrm{ } \pi \textrm{ } l .\)
\(V_{\text{th} \overset{ˊ}{\text{e}} \text{p}} = V_{\text{ngo} \overset{ˋ}{\text{a}} \text{i}} - V_{\text{trong}} = \left(\right. 9 \pi \textrm{ } l \left.\right) \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \left(\right. 7,29 \textrm{ } \pi \textrm{ } l \left.\right) = \left(\right. 9 - 7,29 \left.\right) \textrm{ } \pi \textrm{ } l = 1,71 \textrm{ } \pi \textrm{ } l .\)
Nếu lấy \(\pi = 3,14\), thì
\(V_{\text{th} \overset{ˊ}{\text{e}} \text{p}} = 1,71 \times 3,14 \times l = 5,3694 \textrm{ } l \&\text{nbsp}; \left(\right. \text{cm}^{3} \left.\right) .\)
→ Vậy thể tích phần thép (vỏ ống) là
\(\boxed{V = 1,71 \textrm{ } \pi \textrm{ } l \&\text{nbsp}; \approx 5,3694 \textrm{ } l \&\text{nbsp}; \left(\right. \text{cm}^{3} \left.\right) .}\)
(Thay giá trị chiều dài \(l\) vào để ra kết quả số.)