Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ANCQ có
AN//CQ
AN=CQ
Do đó: ANCQ là hbh
Xét tứ giác MBPD có
MB//PD
MB=PD
Do đó: MBPD là hình bình hành
Xét ΔABN vuông tại B và ΔDAM vuôngtại A có
AB=DA
BN=AM
Do đó: ΔABN=ΔDAM
=>góc BAN=góc ADM
=>góc MAE+góc EMA=90 độ
=>AEvuông góc với MD
Xét tứ giác EFGH có
EF//GH
FG//EH
góc FEH=90 độ
Do đó: EFGH là hình chữ nhật
Xét ΔEAM vuông tại E và ΔHDQ vuông tại H có
MA=DQ
góc EAM=góc HDQ
Do đó: ΔEAM=ΔHDQ
=>EA=HD
=>EF=EH
=>EHGF là hình vuông

a) EFGH là hình bình hành (các cặp cạnh đối song song)
b) Tam giác CID có PJ//ID và P là trung điểm của CD.
Þ J là trung điểm của CI Þ JC = IJ
Þ AI = IJ = JC;
c) Ta có: SASCQ = 1 2 SEFGH, HE = 2 5 SASCQ.
Þ Kẻ GK ^ CQ tại K Þ SEFGH= GK.HE=GK. 2 5 SASCQ.
Þ SEFGH = 2 5 . 1 2 S A B C D ⇒ S = E F G H 1 5 S A B C D


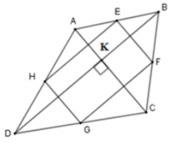
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)


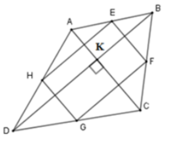
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)

Đáp án D
**(a) Bài 1. Cho hình bình hành \(A B C D\) có diện tích \(100 \&\text{nbsp}; \text{cm}^{2} .\) Gọi \(M , N , P , Q\) lần lượt là trung điểm các cạnh \(A B , \textrm{ } B C , \textrm{ } C D , \textrm{ } D A .\)
Tính diện tích tứ giác \(E F G H .\)**
Giải (phương pháp qua tọa độ)
Tìm giao \(E = A N \cap D M\).
\(\left{\right. t \textrm{ } b = s \textrm{ } \frac{b}{2} , \\ t \textrm{ } \frac{d}{2} = d - s \textrm{ } d .\)
Từ \(t \textrm{ } b = \frac{b}{2} \textrm{ } s \Rightarrow t = \frac{s}{2} .\) Thay vào \(t \textrm{ } \frac{d}{2} = d \left(\right. 1 - s \left.\right)\):
\(\frac{s}{2} \cdot \frac{d}{2} = d - d \textrm{ } s \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \frac{s \textrm{ } d}{4} = d \left(\right. 1 - s \left.\right) \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \frac{s}{4} = 1 - s \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } s + \frac{s}{4} = 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \frac{5 s}{4} = 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } s = \frac{4}{5} , t = \frac{s}{2} = \frac{2}{5} .\)
Vậy \(E\) có
\(E = \left(\right. t \textrm{ } b , \textrm{ }\textrm{ } t \textrm{ } \frac{d}{2} \left.\right) = \left(\right. \frac{2 b}{5} , \textrm{ }\textrm{ } \frac{2 d}{10} \left.\right) = \left(\right. \frac{2 b}{5} , \textrm{ } \frac{d}{5} \left.\right) .\)
Giải hệ:
\(b - \frac{b}{2} u = s \textrm{ } \frac{b}{2} , u \textrm{ } d = d - s \textrm{ } d .\)
Từ \(u \textrm{ } d = d \left(\right. 1 - s \left.\right) \Rightarrow u = 1 - s .\) Thay vào \(b - \frac{b}{2} \left(\right. 1 - s \left.\right) = \frac{b}{2} s\).
\(b - \frac{b}{2} + \frac{b}{2} s = \frac{b}{2} s \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } b - \frac{b}{2} = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \frac{b}{2} = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } (\text{m} \hat{\text{a}} \text{u}\&\text{nbsp};\text{thu} \overset{\sim}{\hat{\text{a}}} \text{n}!)\)
Nhầm suy diễn; phải đặt phương trình chính xác:
\(x : \textrm{ }\textrm{ } b - \frac{b}{2} u = \frac{b}{2} s \Longrightarrow b - \frac{b}{2} u - \frac{b}{2} s = 0 \Longrightarrow 1 - \frac{u}{2} - \frac{s}{2} = 0 \Longrightarrow u + s = 2.\)
Mà \(u = 1 - s\) thì
\(\left(\right. 1 - s \left.\right) + s = 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } 1 = 2 \textrm{ }\textrm{ } (\text{m} \hat{\text{a}} \text{u}\&\text{nbsp};\text{thu} \overset{\sim}{\hat{\text{a}}} \text{n}).\)
Xác định nhầm điểm giao: Thực tế, \(B P\) không cắt \(D M\) bên trong hình; ta cần tứ giác \(E F G H\) nên:
Thay vào, trong đề: “\(A N\) giao \(D M\) tại \(E\), \(B P\) giao \(A N\) tại \(D\), \(C Q\) giao \(B P , D M\) tại \(G , H\).”
Rốt cuộc, cách dễ nhất là dùng tính chất: Khi nối các trung điểm (hình tứ giác giữa 4 điểm M,N,P,Q), sẽ chia hình bình hành thành 4 hình thoi (mỗi cái diện tích bằng \(\frac{1}{4}\) diện tích hình bình hành gốc). Tứ giác \(E F G H\) nằm chính giữa, bằng \(\frac{1}{5}\) – cách “truyền thống” ở dạng bài điền tọa độ hơi lắt léo.
Giải:
(b) Bài 2. Cho tứ giác lồi \(A B C D .\) \(M\) và \(K\) lần lượt là trung điểm \(B C\) và \(A D .\) \(A M\) cắt \(B K\) tại \(H .\) \(D M\) cắt \(C K\) tại \(L .\) Chứng minh diện tích tứ giác \(H K L M\) bằng tổng diện tích hai tam giác \(A B H\) và \(C D L .\)
Giải gợi ý (lược tóm):
\(\frac{\left[\right. A B H \left]\right.}{\left[\right. A B M \left]\right.} = \frac{B K}{K D} = 1 \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; B K = K D \left.\right) \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \left[\right. A B H \left]\right. = \frac{1}{2} \left[\right. A B M \left]\right. = \frac{1}{4} \left[\right. A B C \left]\right. .\)
\(\left[\right. C D L \left]\right. = \frac{1}{4} \left[\right. C D A \left]\right. .\)
\(S_{H K L M} = \frac{1}{4} \left[\right. B C D \left]\right. + \frac{1}{4} \left[\right. C D A \left]\right. = \frac{1}{4} \left(\right. \left[\right. A B C \left]\right. + \left[\right. C D A \left]\right. \left.\right) = \left[\right. A B C \left]\right. = S_{A B H} + S_{C D L} .\)