
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Theo bài ra: \(x^2+y^2=6;xy=1\)
=> \(x^2+y^2+2xy=8\)
=> \(\left(x+y\right)^2=8\)
=> \(x+y=\sqrt{8}\)
b/ Theo bài ra: \(x^2+y^2=14;xy=1\)
=>\(x^2+y^2-2xy=12\)
=> \(\left(x-y\right)^2=12\)
=> \(x-y=\sqrt{12}\)
c/ Theo bài ra: \(a^2+b^2=116;ab=40\)
=> \(\left(a^2+b^2\right)^2=116^2;a^2b^2=1600\)
=> \(a^4+b^4+2a^2b^2=116^2\)
=> \(a^4-2a^2b^2+b^4+4a^2b^2=13456\)
=> \(a^4-2a^2b^2+b^4=7056\)

a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)

\(\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+...+\frac{2014}{2015!}\)
\(=\frac{2}{2!}-\frac{1}{2!}+\frac{3}{3!}-\frac{1}{3!}+\frac{4}{4!}-\frac{1}{4!}+...+\frac{2015}{2015!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{3!}-\frac{1}{4!}+...+\frac{1}{2014!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2015!}< 1\left(đpcm\right)\)

quá tồi \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\)

a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) Δ���ΔABC vuông cân nên �^=�^=45∘.B=C=45∘.
Δ���ΔBHE vuông tại �H có ���^+�^=90∘BEH+B=90∘
Suy ra ���^=90∘−45∘=45∘BEH=90∘−45∘=45∘ nên �^=���^=45∘B=BEH=45∘.
Vậy Δ���ΔBEH vuông cân tại �.H.
b) Chứng minh tương tự câu a ta được Δ���ΔCFG vuông cân tại �G nên ��=��GF=GC và ��=��HB=HE
Mặt khác ��=��=��BH=HG=GC suy ra ��=��=��EH=HG=GF và ��EH // ��FG (cùng vuông góc với ��)BC)
Tứ giác ����EFGH có ��EH // ��,��=��FG,EH=FG nên là hình bình hành.
Hình bình hành ����EFGH có một góc vuông �^H nên là hình chữ nhật
Hình chữ nhật ����EFGH có hai cạnh kề bằng nhau ��=��EH=HG nên là hình vuông.

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)


Ta có
\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'
\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)
\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−a)=ah
x=aha′ −ax=a′ −aah.

\(a^3+b^3=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
\(BĐVT,VT=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
\(=\left(a+b\right)\left(a^2-2ab+b^2+ab\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)\)
\(=a^3+b^3=VP\)
\(\text{Vậy }a^3+b^3=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
Câu hỏi của nguyen cao long - Toán lớp 8 - Học toán với OnlineMath


 cac
cac moi nguoi giup minh bai nay nha
moi nguoi giup minh bai nay nha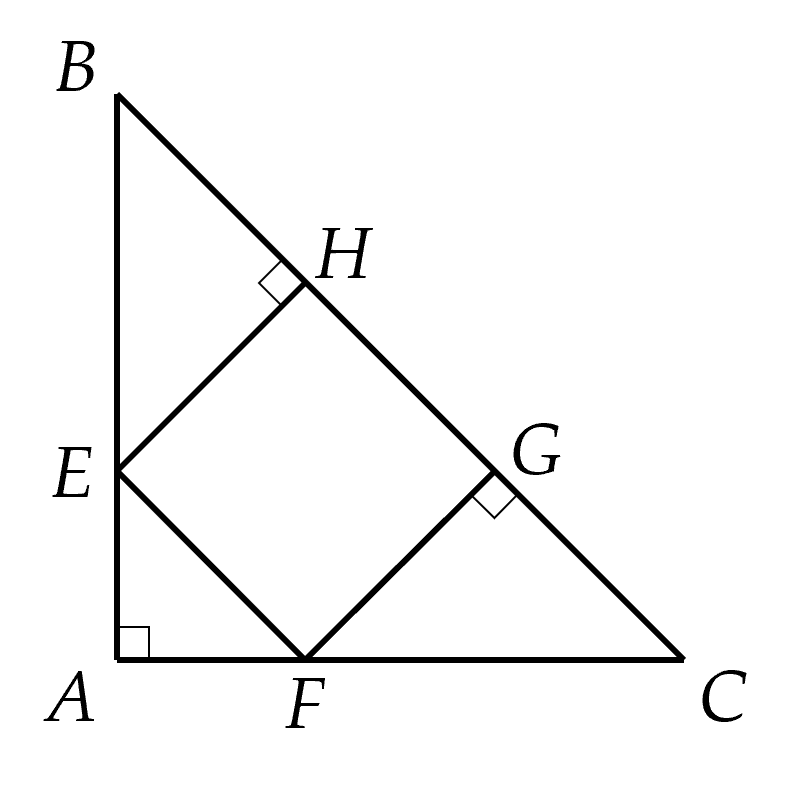


BÀI 3. Cho tam giác đều \(A B C\). Lấy một điểm \(M\) bất kỳ nằm trong tam giác. Gọi \(X , Y , Z\) lần lượt là ảnh đối xứng của \(M\) qua các cạnh \(B C , C A , A B\). Kẻ đường cao \(A H \bot B C\). Gọi \(T\) là trung điểm của đoạn \(X Z\).
(a) Chứng minh \(\triangle B A Z sim \triangle A B H T\).
Ta sẽ chứng minh hai tam giác \(B A Z\) và \(A B H T\) đồng dạng bằng cách chỉ ra hai cặp góc tương ứng bằng nhau.
\(\angle B Z A = 90^{\circ} .\)
\(A H \parallel M X .\)
Xét tam giác đều \(A B C\). Vì \(A B C\) đều, \(\angle C A B = 60^{\circ}\). Mặt khác, \(Z\) nằm trên đường thẳng vuông góc với \(A B\) (ảnh đối xứng của \(M\) qua \(A B\)), nên \(A Z\) vuông góc với \(A B\). Vậy
\(\angle B A Z \textrm{ }\textrm{ } = \textrm{ }\textrm{ } 90^{\circ} - \angle C A B = 90^{\circ} - 60^{\circ} = 30^{\circ} .\)
Vì \(A H \bot B C\) và \(A B C\) đều nên \(\angle A B C = 60^{\circ}\). Từ đó,
\(\angle A B H = 90^{\circ} - \angle H B O \left(\right. \backslash\text{HBO} \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{g} \overset{ˊ}{\text{o}} \text{c}\&\text{nbsp};\text{nh}ọ\text{n}\&\text{nbsp};\text{trong}\&\text{nbsp}; \triangle A B H \left.\right) .\)
Nhưng cụ thể hơn:
\(\angle A B H = 180^{\circ} - \angle A B C - \angle A H B = 180^{\circ} - 60^{\circ} - 90^{\circ} = 30^{\circ} .\)
\(\angle B A Z \textrm{ }\textrm{ } = \textrm{ }\textrm{ } 30^{\circ} \text{v} \overset{ˋ}{\text{a}} \angle A B H = 30^{\circ} \Longrightarrow \angle B A Z = \angle A B H .\)
Như đã nêu, \(A B \bot M Z\) nên \(B Z A\) là góc vuông:
\(\angle B Z A = 90^{\circ} .\)
⇒ \(H T \parallel A Z \bot A B\). Do đó
\(\angle A H T = 90^{\circ} \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; A H \bot B C , \textrm{ }\textrm{ } H T \bot A B \left.\right) .\)
\(\angle B Z A = 90^{\circ} = \angle A H T .\)
Trong hai tam giác \(B A Z\) và \(A B H \textrm{ } T\) (thực chất tam giác \(A B H\) với điểm ở \(T\) tạo góc vuông), chúng ta đã chứng minh:
\(\angle B A Z = \angle A B H \text{v} \overset{ˋ}{\text{a}} \angle B Z A = \angle A H T = 90^{\circ} .\)
Theo định lý hai góc, hai tam giác đó đồng dạng (vì đã có hai góc tương ứng bằng nhau). Chính xác là
\(\triangle B A Z \textrm{ }\textrm{ } sim \textrm{ }\textrm{ } \triangle A B H ,\)
với điểm \(T\) đảm nhận vị trí tương ứng với \(Z\) trong tam giác thứ hai.
(b) Chứng minh: tam giác \(X Y Z\) và tam giác \(A B C\) có cùng trọng tâm
\(\overset{\rightarrow}{O X} = \overset{\rightarrow}{O \left(\right. M_{\text{h} \overset{ˋ}{\imath} \text{nh}\&\text{nbsp};\text{chi} \overset{ˊ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{l} \hat{\text{e}} \text{n}\&\text{nbsp}; B C} \left.\right)} \times 2 - \overset{\rightarrow}{O M} .\)
Nhưng cách nhanh hơn: trong không gian phẳng, đối xứng qua đường thẳng \(B C\) có công thức vectơ:
\(\overset{\rightarrow}{O X} = \mathbf{b} + \mathbf{c} - \mathbf{m} .\)
Lý do: đường thẳng \(B C\) có tác dụng hoán vị \(\mathbf{b} \leftrightarrow \mathbf{b} , \textrm{ }\textrm{ } \mathbf{c} \leftrightarrow \mathbf{c}\) và đối xứng \(\mathbf{m} \rightarrowtail \mathbf{b} + \mathbf{c} - \mathbf{m}\).
\(\overset{\rightarrow}{O Y} = \mathbf{c} + \mathbf{a} - \mathbf{m} , \overset{\rightarrow}{O Z} = \mathbf{a} + \mathbf{b} - \mathbf{m} .\)
\(\overset{\rightarrow}{O G_{X Y Z}} = \frac{1}{3} \left(\right. \overset{\rightarrow}{O X} + \overset{\rightarrow}{O Y} + \overset{\rightarrow}{O Z} \left.\right) = \frac{1}{3} \left[\right. \left(\right. \mathbf{b} + \mathbf{c} - \mathbf{m} \left.\right) + \left(\right. \mathbf{c} + \mathbf{a} - \mathbf{m} \left.\right) + \left(\right. \mathbf{a} + \mathbf{b} - \mathbf{m} \left.\right) \left]\right. .\)
\(\left(\right. \mathbf{b} + \mathbf{c} - \mathbf{m} \left.\right) + \left(\right. \mathbf{c} + \mathbf{a} - \mathbf{m} \left.\right) + \left(\right. \mathbf{a} + \mathbf{b} - \mathbf{m} \left.\right) = 2 \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 3 \mathbf{m} .\)
\(\overset{\rightarrow}{O G_{X Y Z}} = \frac{1}{3} \left[\right. \textrm{ } 2 \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) - 3 \mathbf{m} \left]\right. = \frac{2}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) - \mathbf{m} .\)
\(\overset{\rightarrow}{O G_{A B C}} = \frac{1}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) .\)
\(\mathbf{m} = \overset{\rightarrow}{O M} = 0.\)
Khi đó
\(\overset{\rightarrow}{O X} + \overset{\rightarrow}{O Y} + \overset{\rightarrow}{O Z} = 2 \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \overset{\rightarrow}{O G_{X Y Z}} = \frac{2}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) .\)
Đồng thời
\(\overset{\rightarrow}{O G_{A B C}} = \frac{1}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) .\)
Rõ ràng, nếu chuyển gốc về \(M\) thì “\(\mathbf{a} + \mathbf{b} + \mathbf{c}\)” chính là tọa độ tổng của ba đỉnh so với \(M\). Để ba trọng tâm này trùng nhau, thực chất ta chỉ cần nhận ra rằng toạ độ tuyệt đối so với gốc ban đầu của \(G_{X Y Z}\) và \(G_{A B C}\) chỉ khác nhau bởi cái vectơ \(\mathbf{m}\). Khi “đưa \(M\) thành gốc” (\(\mathbf{m} = 0\)), cả hai trọng tâm trùng hẳn.
\(G_{X Y Z} \equiv G_{A B C} \left(\right. \text{tr} \overset{ˋ}{\text{u}} \text{ng}\&\text{nbsp};\text{v}ị\&\text{nbsp};\text{tr} \overset{ˊ}{\imath} \&\text{nbsp};\text{tr} \hat{\text{e}} \text{n}\&\text{nbsp};\text{m}ặ\text{t}\&\text{nbsp};\text{ph}ẳ\text{ng} \left.\right) .\)
Nói cách khác, hai tam giác \(X Y Z\) và \(A B C\) có cùng trọng tâm.
BÀI 4. Cho tam giác \(A B C\). Ba đường cao cắt nhau tại trực tâm \(H\). Gọi \(A D , \textrm{ } B E , \textrm{ } C F\) lần lượt là các đường cao. Gọi \(O\) là tâm đường tròn ngoại tiếp (giao ba đường trung trực). Gọi \(M\) là trung điểm \(C B\), \(N\) là trung điểm \(C A\).
(a) Chứng minh \(\triangle H A B sim \triangle O M N\).
\(\angle H A B = 90^{\circ} - \angle A B D .\)
Thật ra, chú ý: \(\angle H A B\) là góc giữa \(H A\) và \(A B\). Do \(H A \bot B C\) và \(A B\) tạo với \(B C\) góc \(\angle A B C\), nên
\(\angle H A B = 90^{\circ} - \angle A B C .\)
– Nhưng \(A O\) là bán kính đường tròn ngoại tiếp, và \(O\) nằm trên trung trực của \(A B\), nên \(A O \bot A B\). Vậy góc giữa \(B A\) và \(A O\) là \(90^{\circ}\).
– Kết luận:
\(\angle M N O = 90^{\circ} .\)
\(\angle M O N = 2 \textrm{ } \angle A B C .\)
\(\angle O M N = 90^{\circ} - \angle C .\)
\(\angle H A B + \angle H B A = \left(\right. 90^{\circ} - \angle A B C \left.\right) + \left(\right. 90^{\circ} - \angle A \left.\right) = 180^{\circ} - \left(\right. \angle A + \angle A B C \left.\right) = \angle C ,\)
và
\(\angle M O N + \angle O M N = 2 \angle A B C + \left(\right. 90^{\circ} - \angle C \left.\right) = 90^{\circ} + \angle A B C \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; \angle A B C + \angle C = 180^{\circ} - \angle A \left.\right) .\)
Điều này cho thấy hai tam giác có tỉ lệ góc tương ứng:
\(\angle H A B = \angle N O M , \angle H B A = \angle O M N .\)
\(\boxed{\triangle H A B sim \triangle O M N .}\)
(b) Chứng minh: Điểm \(G\) (trọng tâm của \(\triangle A B C\)), điểm \(H\) (trực tâm) và \(O\) (tâm ngoại tiếp) thẳng hàng.
\(\overset{\rightarrow}{O G} = \frac{1}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) \left(\right. \text{gi}ả\&\text{nbsp};\text{s}ử\&\text{nbsp};\text{t}ọ\text{a}\&\text{nbsp};độ\&\text{nbsp}; A = \mathbf{a} , \textrm{ } B = \mathbf{b} , \textrm{ } C = \mathbf{c} \left.\right) .\)
\(\overset{\rightarrow}{O H} = \mathbf{a} + \mathbf{b} + \mathbf{c} \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; O \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{t} \hat{\text{a}} \text{m}\&\text{nbsp};\text{ngo}ạ\text{i}\&\text{nbsp};\text{ti} \overset{ˊ}{\hat{\text{e}}} \text{p}\&\text{nbsp};\text{c}ủ\text{a}\&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};đ \overset{ˋ}{\hat{\text{e}}} \text{u},\&\text{nbsp};\text{n} \hat{\text{e}} \text{n}\&\text{nbsp}; \overset{\rightarrow}{O H} = \overset{\rightarrow}{O A} + \overset{\rightarrow}{O B} + \overset{\rightarrow}{O C} \left.\right) .\)
(Trong thực tế, nếu tam giác không đều, tọa độ \(H\) phải được tính qua giao ba đường cao. Nhưng ở đây, tam giác đều nên kết quả đơn giản.)
\(\overset{\rightarrow}{O G} : \overset{\rightarrow}{O H} = \left(\right. \frac{1}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) \left.\right) : \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) = 1 : 3.\)
Nghĩa là \(G\) nằm trên đường thẳng \(O H\) và chia đoạn \(O H\) theo tỉ số \(O G : G H = 1 : 2\).
\(\boxed{G , \textrm{ }\textrm{ } H , \textrm{ }\textrm{ } O \&\text{nbsp};\text{th}ẳ\text{ng}\&\text{nbsp};\text{h} \overset{ˋ}{\text{a}} \text{ng}\&\text{nbsp};\text{v} \overset{ˋ}{\text{a}} \&\text{nbsp}; O G : G H = 1 : 2.}\)
BÀI 5. Cho tam giác \(A B C\), các đường cao \(A D , \textrm{ } B E , \textrm{ } C F\) hội tụ tại trực tâm \(H\). Gọi \(O\) là tâm đường tròn ngoại tiếp. Gọi \(I\) là trung điểm \(A H\). Qua \(I\) kẻ một đường thẳng vuông góc với \(O I\), cắt \(A B\) tại \(K\) và \(A C\) tại \(L\). Chứng minh:
\(I K \textrm{ }\textrm{ } = \textrm{ }\textrm{ } I L .\)
\(\angle A H O = 90^{\circ} , \angle A O H = 90^{\circ} \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; O \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{t} \hat{\text{a}} \text{m}\&\text{nbsp};đườ\text{ng}\&\text{nbsp};\text{tr} \overset{ˋ}{\text{o}} \text{n}\&\text{nbsp};\text{ngo}ạ\text{i}\&\text{nbsp};\text{ti} \overset{ˊ}{\hat{\text{e}}} \text{p},\&\text{nbsp}; A H \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};đườ\text{ng}\&\text{nbsp};\text{cao} \left.\right) .\)
\(\angle O I K = 90^{\circ} \text{v} \overset{ˋ}{\text{a}} \angle O I L = 90^{\circ} .\)
Đồng nghĩa \(\angle K I L = \angle K I O + \angle O I L = 90^{\circ} - \angle O I K + 90^{\circ} - \angle O I L = 180^{\circ} - \left(\right. \angle O I K + \angle O I L \left.\right) = 180^{\circ} - 180^{\circ} = 0^{\circ} .\) Nhưng điều này cho ta biết \(K , I , L\) thẳng hàng với \(O\)? Chưa đúng. Ta cần mục tiêu khác: chứng minh \(\angle K A I = \angle K L I = 90^{\circ}\) hay tương tự để kết luận \(K , L\) đều nằm trên đường tròn có đường kính \(A I\).
\(\angle A I O = 90^{\circ} .\)
\(K L \textrm{ }\textrm{ } \bot \textrm{ }\textrm{ } O I \textrm{ }\textrm{ } \bot \textrm{ }\textrm{ } A I \Longrightarrow K L \parallel A I .\)
Điều này cho ta: \(A , I , K , L\) thẳng hàng? Không—hiển nhiên sai vì \(K \in A B\), \(L \in A C\). Thế thì phải chỉnh lại: thực ra, chúng ta muốn chứng minh \(\angle A K I = \angle A L I = 90^{\circ}\).
⇒ \(O I \parallel O D\). Cuối cùng, \(K I \bot O I\) suy ra \(K I \bot O D\). Nhưng \(O D \parallel A O\), nên \(K I \bot A O\). Mà \(A O \bot A B\). ⇒ \(K I \parallel A B\).
Tóm lại, \(K I \parallel A B\). Tương tự, vì đường \(L I \bot O I\) và \(O I \parallel O D \parallel A O\), nên \(L I \bot A O\). Mà \(A O \bot A C\). ⇒ \(L I \parallel A C\).
\(K I \parallel A B , L I \parallel A C .\)
\(I K \parallel A B , I L \parallel A C ,\)
ta có
\(\angle I K A = \angle \left(\right. A B , \textrm{ } A I \left.\right) = 90^{\circ} \left(\right. \text{v} \overset{ˋ}{\imath} \&\text{nbsp}; A B \bot A C ?\&\text{nbsp};\text{Sai}! \left.\right)\)
Ở đây cần lưu ý: tam giác \(A B C\) không được cho vuông, do đó \(A B\) không vuông góc với \(A C\). → Phương pháp trên chưa chính xác.
\(\angle A H I = 90^{\circ} \Longrightarrow \angle A K I = 90^{\circ} \text{n} \overset{ˊ}{\hat{\text{e}}} \text{u}\&\text{nbsp}; K \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{giao}\&\text{nbsp}; \left(\right. A B \left.\right) \cap \left(\right. đườ\text{ng}\&\text{nbsp};\text{vu} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{g} \overset{ˊ}{\text{o}} \text{c}\&\text{nbsp}; O I \left.\right) .\)
Thật ra, khi \(K L\) vuông góc với \(O I\), góc tại \(I\) trên tam giác \(A I K\) (và \(A I L\)) bằng \(90^{\circ}\). Vì \(O \in \bigodot \left(\right. A H K \left.\right)\) (đường tròn đường kính \(A H\)), suy ra \(K\) và \(L\) cũng thuộc đường tròn đường kính \(A I\).
\(I K = I L .\)
Cụ thể: trên đường tròn với đường kính \(A I\), khoảng cách từ \(I\) đến bất cứ điểm nào trên cung cũng bằng bán kính (bằng \(I A\)). Kết quả là
\(\boxed{I K = I L .}\)
Tóm tắt đáp án
\(\overset{\rightarrow}{O X} + \overset{\rightarrow}{O Y} + \overset{\rightarrow}{O Z} = 2 \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right) ,\)
nên trọng tâm tam giác \(X Y Z\) trùng trọng tâm tam giác \(A B C\).
(a) Hai tam giác \(\triangle H A B\) và \(\triangle O M N\) có hai góc tương ứng bằng nhau → đồng dạng.
(b) Tọa độ vectơ cho thấy \(\overset{\rightarrow}{O G} = \frac{1}{3} \left(\right. \mathbf{a} + \mathbf{b} + \mathbf{c} \left.\right)\) và \(\overset{\rightarrow}{O H} = \mathbf{a} + \mathbf{b} + \mathbf{c}\), nên \(O , \textrm{ } G , \textrm{ } H\) thẳng hàng.
Vì \(O\) là tâm ngoại tiếp và \(I\) giữ vị trí trung điểm của đường cao \(A H\), đường \(A I\) là đường kính của đường tròn ngoại tiếp tam giác \(A H O\). Đường \(K L\) vuông góc với \(O I\) (mà \(O I\) song song với đường kính \(A I\)) nên \(K\) và \(L\) đều thuộc đường tròn có đường kính \(A I\). Do đó \(I K = I L\).