K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

16 tháng 2 2021

bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!

19 tháng 6 2023
a: CD vuông góc DA
CD vuông góc SA
=>CD vuông góc (SAD)
=>CD vuông góc SD
b: CD vuông góc AK
AK vuông góc SD
=>AK vuông góc (SCD)
=>SC vuông góc AK
BC vuông góc AH
AH vuông góc SB
=>AH vuông góc SC
=>SC vuông góc (AKH)
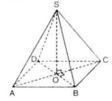
c: (SO;(ABCD))=(OS;OA)=góc SOA

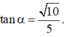







Mình sẽ giải chi tiết bài toán hình học không gian này nhé:
Bài toán:
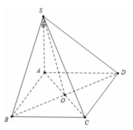
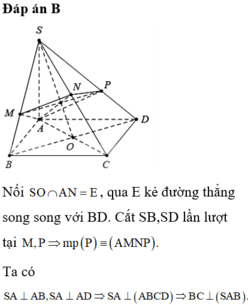
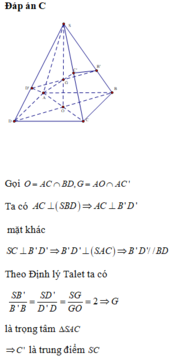
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O với OA = 2OB = 2a và SO ⊥ đáy (ABCD). Mặt phẳng (a) qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Biết tam giác B'C'D' đều. Tính cos góc giữa mặt phẳng (SAB) và mặt phẳng (a).
Bước 1: Xác định tọa độ các điểm
Để dễ tính toán, ta đặt hệ trục tọa độ như sau:
Ta giả sử:
Do ABCD là hình thoi, 4 điểm này tạo thành hình thoi với tâm O.
Bước 2: Xác định điểm S
Bước 3: Tìm phương trình mặt phẳng (a)
Vậy phương trình mặt phẳng (a):
\(- 2 a \left(\right. x - 2 a \left.\right) + 0 \left(\right. y - 0 \left.\right) - h \left(\right. z - 0 \left.\right) = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } - 2 a x + 4 a^{2} - h z = 0\)
Hay:
\(2 a x + h z = 4 a^{2}\)
Bước 4: Tìm giao điểm B', C', D' trên SB, SC, SD
Vector SB = B - S = (a, b, -h)
Điểm B' trên SB có dạng:
\(B^{'} = S + t \cdot \overset{\rightarrow}{S B} = \left(\right. t a , t b , h - t h \left.\right)\)
\(C^{'} = S + s \cdot \overset{\rightarrow}{S C} = \left(\right. 0 , 0 , h \left.\right) + s \left(\right. - 2 a , 0 , - h \left.\right) = \left(\right. - 2 a s , 0 , h - h s \left.\right)\)
Vector SD = D - S = (-a, -b, -h)
Điểm D':
\(D^{'} = S + r \cdot \overset{\rightarrow}{S D} = \left(\right. - a r , - b r , h - h r \left.\right)\)
Bước 5: Tìm giao điểm với mặt phẳng (a)
Các điểm B', C', D' nằm trên mặt phẳng (a):
\(2 a x + h z = 4 a^{2}\)
Thay tọa độ các điểm vào:
\(2 a \cdot \left(\right. t a \left.\right) + h \left(\right. h - t h \left.\right) = 4 a^{2}\) \(2 a^{2} t + h^{2} - h^{2} t = 4 a^{2}\) \(t \left(\right. 2 a^{2} - h^{2} \left.\right) = 4 a^{2} - h^{2}\) \(t = \frac{4 a^{2} - h^{2}}{2 a^{2} - h^{2}}\)
\(2 a \left(\right. - 2 a s \left.\right) + h \left(\right. h - h s \left.\right) = 4 a^{2}\) \(- 4 a^{2} s + h^{2} - h^{2} s = 4 a^{2}\) \(s \left(\right. - 4 a^{2} - h^{2} \left.\right) = 4 a^{2} - h^{2}\) \(s = \frac{4 a^{2} - h^{2}}{- 4 a^{2} - h^{2}}\)
\(2 a \left(\right. - a r \left.\right) + h \left(\right. h - h r \left.\right) = 4 a^{2}\) \(- 2 a^{2} r + h^{2} - h^{2} r = 4 a^{2}\) \(r \left(\right. - 2 a^{2} - h^{2} \left.\right) = 4 a^{2} - h^{2}\) \(r = \frac{4 a^{2} - h^{2}}{- 2 a^{2} - h^{2}}\)
Bước 6: Điều kiện tam giác B'C'D' đều
Từ tọa độ B', C', D', ta tính độ dài các đoạn B'C', C'D', D'B' và thiết lập điều kiện bằng nhau để tìm h.
Do khá phức tạp, bạn có thể cho mình biết có cần mình tiếp tục giải chi tiết phần này không nhé?
Bước 7: Tính cos góc giữa (SAB) và (a)
\(cos \theta = \frac{\mid \overset{⃗}{n_{1}} \cdot \overset{⃗}{n_{2}} \mid}{\mid \overset{⃗}{n_{1}} \mid \cdot \mid \overset{⃗}{n_{2}} \mid}\)
Nếu bạn muốn, mình có thể tiếp tục phần tính cos góc hoặc giải chi tiết phần tam giác đều. Bạn chỉ cần nói nhé!