Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
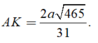

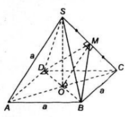
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
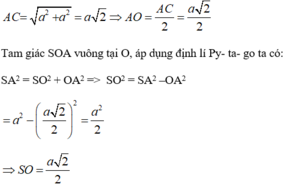

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
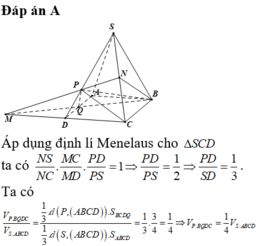

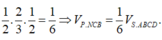

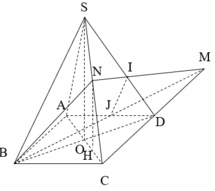
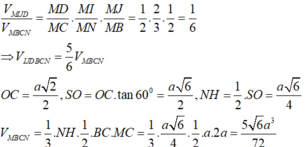
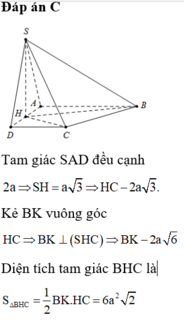
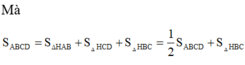
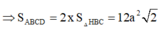
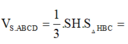
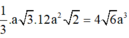
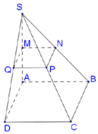
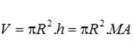
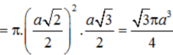
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên SA,…, SD hợp với mặt đáy góc 60°. Gọi O là tâm đáy, M đối xứng với C qua D, N trung điểm SC. Tính khoảng cách từ O đến mặt phẳng (SAD).
Kết quả: