Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
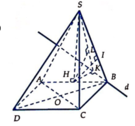
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
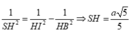
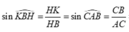
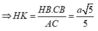
![]()
![]()
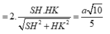

\(\left(SAB\right);\left(SAC\right)\) cùng vuông góc (ABCD) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{3}\)
Gọi M là trung điểm CD \(\Rightarrow GS=\dfrac{2}{3}MS\) (t/c trọng tâm)
\(\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{2}{3}d\left(M;\left(SBD\right)\right)\)
Gọi I là giao điểm AM và BD \(\Rightarrow\dfrac{IM}{IA}=\dfrac{DM}{AB}=\dfrac{1}{2}\)
\(\Rightarrow d\left(M;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{1}{3}d\left(A;\left(SBD\right)\right)\)
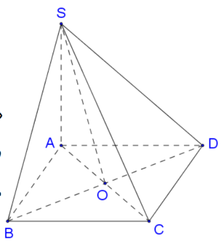
Kẻ AH vuông góc SO (O là tâm đáy) \(\Rightarrow AH\perp\left(SBD\right)\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
\(\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{1}{3}AH=\dfrac{a\sqrt{21}}{21}\)

Đáp án B.
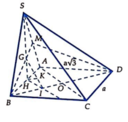
Gọi H là trung điểm AB, G là trọng tâm
Trong mặt phẳng (ABCD), ![]()
Ta có: ![]()
Gọi I là hình chiếu của H lên BD, K là hình chiếu của H lên GI
![]()
Ta có: 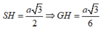
![]()
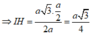
![]()
![]()
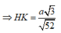
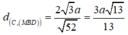
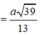

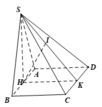
Do SAB là tam giác đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi E là trung điểm CD, từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\left\{{}\begin{matrix}HE\perp CD\\SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHE\right)\)
\(\Rightarrow CD\perp HF\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(HE=BC=a\) ; \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng:
\(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)

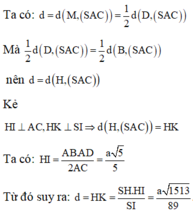
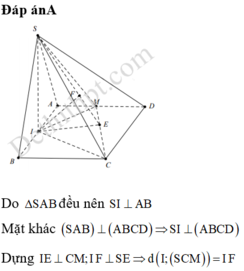
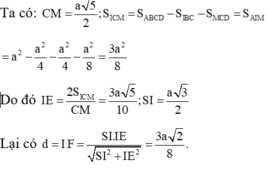
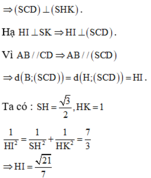
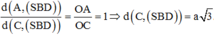


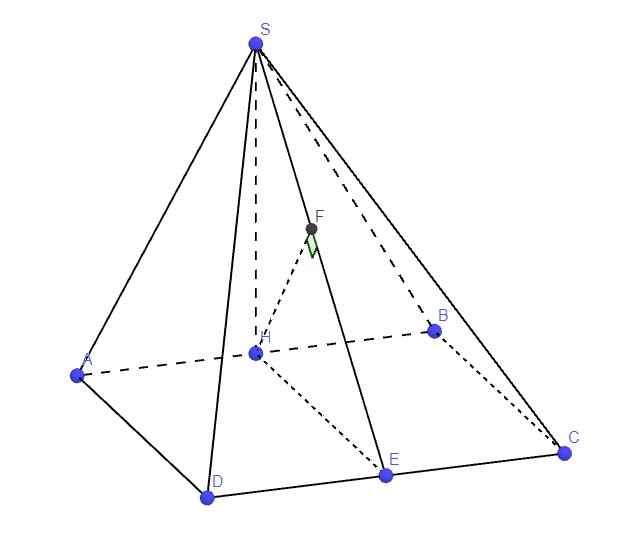
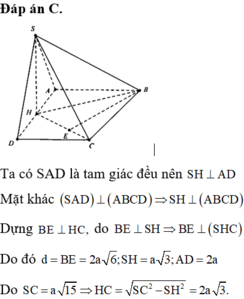
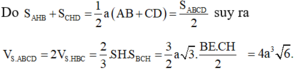
Với bài toán về hình chóp S.ABCD có đáy là hình chữ nhật, trong đó tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, để tính khoảng cách từ điểm A đến mặt phẳng (SBD), bạn cần áp dụng các kiến thức về định lý hình học không gian. Đầu tiên, ta sẽ phân tích vị trí của các điểm và các hình học của tam giác, hình chóp. Sau đó, áp dụng các công thức tính khoảng cách giữa một điểm và mặt phẳng trong không gian.
Tuy nhiên, bài toán này cần sự tính toán chi tiết và có thể sử dụng phương pháp vectơ hoặc phương pháp trực quan qua hình học để giải.