Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ∆ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến
Suy ra BH=CH
Xét ∆AHB và ∆AHC có
AH là cạnh chung
BH=CH (cmt)
AB=AC (∆ABC cân tại A)
Do đó ∆AHB=∆AHC
Xét ∆AMH ta có
AD vuông góc với MH (HD vuông góc AB)
Suy ra AD là đường cao của ∆AMH (1)
DH=DM (gt)
Nên AD là đường trung bình của ∆AMH (2)
Từ (1) và (2) suy ra ∆AMH cân tại A
Suy ra AM=AH

a: ΔBAM cân tại B
mà BE là đường cao
nên BE là phân giác của góc ABM
b: Xét ΔMBA có
AH,BE là đừog cao
AH căt BE tại K
=>K là trực tâm
=>MK vuông gócAB
=>MK//AC

Ta có: góc MAC=góc NBC( góc CAB=góc CBA) mà góc MAC+ góc CAB=180o
góc NBC+góc CBA=180o
Xét tam giác CAM và tam giác CBN:
MA=BN(gt)
góc MAC=góc NBC(cmt)
CA=CB(gt)
=> tam giác CAM= tam giác CBN(c-g-c)
=> Góc MCA=góc NCB(góc tương ứng)
Xét tam giác CHA và tam giác CKB
CA=CB(gt)
Góc MCA=góc NCB(góc tương ứng của tam giác CAM= tam giác CBN)
Góc CHA=góc CKB=90o
=> tam giác CHA=tam giác CKB(ch-gn)
=> AH=BK (cạnh tương ứng)
tik nha bn nếu có thể kết bạn lun nhé!

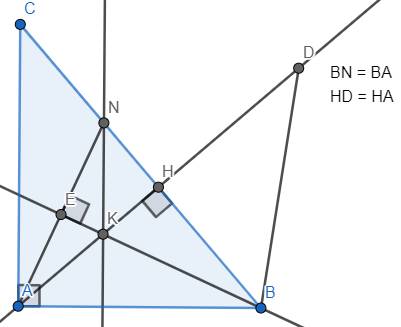
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)