Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Số tam giác có 3 đỉnh là 3 trong 15 điểm đã cho bằng số cách chọn 3 điểm trong 15 điểm đã cho và bằng C 15 3 . (không quan tâm đến thứ tự đỉnh).

+ Phương trình đường thẳng d đi qua A và có hệ số góc k là: y= k( x-a) +1
+ Phương trình hoành độ giao điểm của d và (C) :
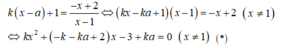
+ Với k= 0, ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
Với k≠0 , d và (C) tiếp xúc nhau khi và chỉ khi (1) có nghiệm kép
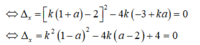
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1) vẽ được đúng tiếp tuyến thì phương trình có đúng một nghiệm k≠ 0.
*Xét 1-a= 0 hay a=1, ta có 4k+ k= 0 hạy k= -1 thỏa.
*Có f(0) = 4≠0 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là .
*Còn lại là trường hợp ∆x= 0 có nghiệm kép khi
![]()
Vậy có 2 giá trị của a thỏa mãn đầu bài là a= 1 hoặc a= 3/2.
Chọn A.

ĐKXĐ: 0 ≤ x ≤ 4 x 2 - 6 x + 2 m > 0
Ta có
12
+
4
x
-
x
2
≠
0
∀
x
nên để ( C) có hai tiệm cận đứng thì phương trình
x
2
-
6
x
+
2
m
=
0
⇔
x
2
-
6
x
+
2
m
=
0
(
*
)
có hai nghiệm phân biệt thuộc [ 0; 4]
Đế phương trình có 2 nghiệm phân biệt thì ∆ ' = 9 - 2 m > 0 ⇔ m < 9 2
Gọi 2 nghiệm phân biệt của (*) là x1< x2 ta có 0≤ x1< x2≤ 4.
Theo định lí Vi-et ta có x 1 + x 2 = 6 x 1 x 2 = 2 m
Khi đó

Kết hợp nghiệm ta có 4 ≤ m ≤ 9 2
Mà m nguyên nên m= 4
Chọn B.

\(\lim\limits_{x\rightarrow+\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\lim\limits_{x\rightarrow+\infty}\dfrac{2019}{\sqrt{17-\dfrac{1}{x^2}}-m}=\dfrac{2019}{\sqrt{17}-m}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\dfrac{2019}{m-\sqrt{17}}\)
Với \(m\ne\sqrt{17}\Rightarrow\) đồ thị hàm số luôn có 2 tiệm cận ngang
Với \(m=\sqrt{17}\) đồ thị hàm số ko có tiệm cận ngang
Xét phương trình: \(\sqrt{17x^2-1}=m\left|x\right|\)
- Với \(m< 0\Rightarrow\) pt vô nghiệm \(\Rightarrow\) ko có tiệm cận đứng \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
- Với \(m\ge0\)
\(\Leftrightarrow17x^2-1=m^2x^2\Leftrightarrow\left(17-m^2\right)x^2=1\)
+ Nếu \(\left[{}\begin{matrix}m\ge\sqrt{17}\\m\le-\sqrt{17}\end{matrix}\right.\) pt vô nghiệm \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
+ Nếu \(-\sqrt{17}< m< \sqrt{17}\) pt có 2 nghiệm \(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy \(m=\left\{0;1;2;3;4\right\}\) có 5 phần tử

Bài toán
Cho tập hợp \(S = \left{\right. 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 \left.\right}\). Hỏi có bao nhiêu cách chia tập \(S\) thành ba tập con khác rỗng sao cho không có tập con nào chứa hai số nguyên liên tiếp.
Phân tích bài toán
Bước 1: Mô hình hóa
Để tránh nhầm lẫn, ta xét cách gán mỗi phần tử \(i \in S\) vào một trong ba tập con \(A , B , C\).
Bước 2: Biến đổi bài toán
Ta có thể xem đây là bài toán gán nhãn cho dãy số từ 1 đến 10 bằng 3 nhãn (A, B, C), sao cho:
Bước 3: Đếm số cách gán nhãn
Bước 4: Đếm số chuỗi nhãn độ dài 10 với 3 kí hiệu, không có 2 kí tự liên tiếp giống nhau
Đây là bài toán đếm số chuỗi độ dài 10 trên 3 kí tự \(\left{\right. A , B , C \left.\right}\), sao cho không có 2 kí tự liên tiếp giống nhau.
Tuy nhiên, trong số này có những chuỗi mà không xuất hiện đủ cả 3 ký tự (có thể chỉ có 1 hoặc 2 ký tự).
Bước 5: Loại bỏ chuỗi không đủ 3 ký tự
Ta cần đếm số chuỗi không có kí tự liên tiếp giống nhau, và có đủ cả 3 kí tự.
Bước 6: Số chuỗi có đủ 3 kí tự và không có 2 kí tự liên tiếp giống nhau
Áp dụng nguyên lý loại trừ:
\(\text{S} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{chu} \overset{\sim}{\hat{\text{o}}} \text{i}\&\text{nbsp};\text{th}ỏ\text{a}\&\text{nbsp};\text{m} \overset{\sim}{\text{a}} \text{n} = 1536 - 6 = 1530\)Bước 7: Xử lý thứ tự tập con (vì chia tập)
Hiện tại, ta đang đếm số chuỗi nhãn cho dãy 1..10, tức là phân chia có thứ tự: \(\left(\right. A , B , C \left.\right)\).
Nhưng bài toán là chia tập thành 3 tập con, không quan trọng thứ tự của 3 tập con.
Kết luận:
Số cách chia tập \(S\) thành 3 tập con khác rỗng, không có tập con nào chứa hai số nguyên liên tiếp là:
\(\frac{1530}{6} = 255\)Đáp số:
\(\boxed{255}\)Nếu bạn cần giải thích thêm hoặc mở rộng bài toán, hãy cho tôi biết nhé!