Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi : 1 lít = 1 \(d{m^3}\) = 1000 \(c{m^3}\)
a)
Chiều rộng của hộp sữa là:
1000: (20 . 10) = 1000 : 200= 5 (cm)
b)
Diện tích vật liệu dùng để làm vỏ hộp sữa là diện tích xung quanh và diện tích của hai mặt đáy của hình hộp.
Diện tích xung quanh của hộp sữa là:
\(\left( {10 + 5} \right).2.20 = 600\left( {c{m^2}} \right)\)
Diện tích của hai mặt đáy là:
\(2.10.5 = 100\left( {c{m^2}} \right)\)
Vậy diện tích vật liệu cần dùng là:
\(600 + 100 = 700\left( {c{m^2}} \right)\)

Diện tích xung quanh của hộp sữa là:
\(\left(4+5\right)\times2\times12=216\left(cm^2\right)\)
Thể tích của hộp sữa là:
\(4\times5\times12=240\left(cm^3\right)\)
Diện tích xung quanh của hộp sữa là:
Sxq = (4 + 5) . 2 . 12 = 216 cm2
Thể tích hộp sữa là:
V = 4 . 5 . 12 = 240 cm3

Đổi \(1l=1dm^3=1000cm^3\)
a. Chiều rộng: \(1000:10:20=5cm\)
b. Diện tích xung quanh: \(\left(5+10\right)\times2\times20=600cm^2\)
DIện tích vật liệu dùng \(600+5\times10\times2=700cm^2\)

Thể tích của hộp chữ nhật được tính theo công thức: V = chiều dài x chiều rộng x chiều cao.
Theo đề bài, chiều cao là 1 (cm), chiều rộng là x (cm) và chiều dài hơn chiều rộng là 3 (cm).
Do đó, chiều dài là x + 3 (cm).
Thay giá trị vào công thức, ta có:
V = (x + 3) x x x 1
= x(x + 3)
Do đó, thể tích của hộp chữ nhật được tính theo x là V = x(x + 3).
...

Tham khảo:
Ta có thể tích hình hộp chữ nhật bằng tích chiều cao và diện tích đáy
Nên chiều rộng của hình chữ nhật = thể tích : ( chiều cao . chiều dài )
Diện tích đáy là \((x + 5)(x + 1) = {x^2} + 6x + 5\)
Thay các số ở đề bài cho vào công thức trên ta được :
\( = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{(x + 5)(x + 1) = {x^2} + 6x + 5}} = \dfrac{{3{x^3} + 8{x^2} - 45x - 50}}{{{x^2} + 6x + 5}}\)

Vậy chiều dài hình hộp chữ nhật là 3x – 10 cm

Diện tích mặt đáy của hình hộp chữ nhật là:
\((x + 1).(x + 2) = x(x + 2) + 1.(x + 2)\\ = {x^2} + 2x + x + 2 = {x^2} + 3x + 2\) \((c{m^2})\).
Vậy chiều cao của hình hộp chữ nhật đó theo x là:
\(({x^3} + 6{x^2} + 11x + 6):({x^2} + 3x + 2) = x + 3\)(cm).

Diện tích 2 đáy:
\(25\cdot12=300\left(cm^2\right)\)
Diện tích xung quanh:
\(\left(25+12\right)\cdot2\cdot10=740\left(cm^2\right)\)
Diện tích làm hộp giấy ăn:
\(740+300=1040\left(cm^2\right)\)
Diện tích 2 đáy là:
25⋅12=300(��2)25⋅12=300(cm2)
Diện tích xung quanh là:
(25+12)⋅2⋅10=740(��2)(25+12)⋅2⋅10=740(cm2)
Diện tích làm hộp giấy ăn là:
740+300=1040(��2)740+300=1040(cm2)
Đáp số: 1040 Diện tích 2 đáy:
25⋅12=300(��2)25⋅12=300(cm2)
Diện tích xung quanh:
(25+12)⋅2⋅10=740(��2)(25+12)⋅2⋅10=740(cm2)
Diện tích làm hộp giấy ăn:
740+300=1040(��2)740+300=1040(cm2)

a)
Thể tích của hộp là :
\(20.14.15 = 4200\left( {c{m^3}} \right)\)
b)
Diện tích bìa để làm hộp bằng diện tích xung quanh + diện tích 2 mặt đáy của hình hộp chữ nhật.
Diện tích bìa dùng làm hộp là:
\(2.\left( {14 + 20} \right).15 + 2.20.14 = 1580\left( {c{m^2}} \right)\)

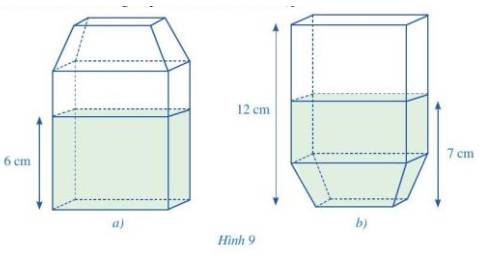
Xét hình 9b, phần hộp không chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 12 – 7 = 5 (cm)
Xét hình 9a, phần hộp chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 6 cm.
Do đó, trong hình 9a, phần hộp chứa sữa chiếm 6 phần, phần không chứa sữa chiếm 5 phần, thể tích cả hộp là: 5+6 = 11 phần.
Như vậy, tỉ số của của thể tích sữa có trong hộp và thể tích của cả hộp là \(\frac{6}{{11}}\).

Chiều rộng hình hộp chữ nhật đó là:
\(680:2:10-20=12\) ( cm )
Đ/S:.
**Câu 1:** Để tính chiều cao của lượng sữa trong hộp, trước tiên, ta cần biết thể tích của hộp sữa bằng 1 lít, tức là 1000 cm³.
Thể tích của hình hộp chữ nhật được tính theo công thức:
\[
V = chiều \, dài \times chiều \, rộng \times chiều \, cao
\]
Với chiều ngang (chiều rộng) là 10 cm, chiều sâu (chiều dài) là 15 cm và chiều cao là 22 cm. Ta có:
\[
V = 10 \times 15 \times h
\]
Khi sữa có thể tích là 1 lít (1000 cm³), ta có:
\[
10 \times 15 \times h = 1000
\]
Tính \(h\):
\[
150h = 1000
\]
\[
h = \frac{1000}{150} \approx 6.67 \, cm
\]
Vậy chiều cao của lượng sữa trong hộp là khoảng 6.67 cm.
**Câu 2:** Hình được ghép bởi 8 hình tam giác có thể là hình octagon (hình bát giác) hoặc hình hình chữ nhật, tùy vào cách sắp xếp các tam giác. Trong nhiều trường hợp, nếu 8 tam giác được xếp một cách hợp lý, chúng có thể tạo thành hình tròn hoặc các biến thể của các nhiều giác khác. Cụ thể hơn cần có hình minh họa để xác định.