Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A/ Theo giả thiết ta có:DA=BA;AE=AC\(\Rightarrow\) DC=BE
Vì tam giác BDA là tam giác vuông cân\(\Rightarrow\)góc A=90 độ\(\Rightarrow\) DC vuông góc vs BE
B/ Áp dụng định lý Pi-ta-go cho tam giác BAD vuông tại A:BD2=BA2+AD2
ACE vuông tại A:CE2=AC2+AE2
ADE vuông tại A:DE2=DA2+AE2
BAC vuông tại A:BC2=AB2+AC2
Từ trên suy ra:BD2+CE2=BC2+DE2
C/Xét tam giác BAC và DAE:DA=BA
BA=AE
GÓC BAC=GÓC DAE=90
\(\Rightarrow\) Tam giác BAC=DAE(c-g-c)
\(\rightarrow\) BC=DE(2 cạnh t/ứ)
\(\rightarrow\) góc CBA=góc AED(t/ứ)
mà 2 góc nàm vị trí so le trong\(\Rightarrow\)BC song song DE
\(\rightarrow\) góc BCE+góc CED=180 ĐỘ(2 góc phía trong cùng phía)
mà góc DCE=góc BEC(TAM GIÁC cae VUÔNG CÂN)
\(\Rightarrow\) Góc BCD=góc BED
MÀ góc BCD=CDE(so le trong)
\(\Rightarrow\) góc ADE=góc AED\(\Rightarrow\) TAM GIÁC ADE vuông cân tai E
mà ta có AI(IK cắt DE ở I)LÀ đường trung trực của tam giác
\(\rightarrow\) AI cx là đg trung tuyến của ADE
\(\Rightarrow\) I là trung điểm của DE
MÀ ta lại có BC=DE(cm phần trên rồi)
\(\Rightarrow\) k là trung điểm của BC
(ko bít vẽ hình)

Xét tgiac ACE. ADB:
góc A chung
D=E=90¤
AB=AC
=> Tgiac ACE==ABD (c-h-g-n)
=> BD=CE ( 2ctu) và AE=AD ( sử dụng cho cậu c))
b) BD giao CE tại G=> G là trực tâm tgiac ABC
=> AG vuông góc với BC
c) Xét 2 t giác AEG=ADG ( c-h-c-g-v)
=>GE=GD(2ctu) =>GB=GC=> tgiac GBC cân tại B

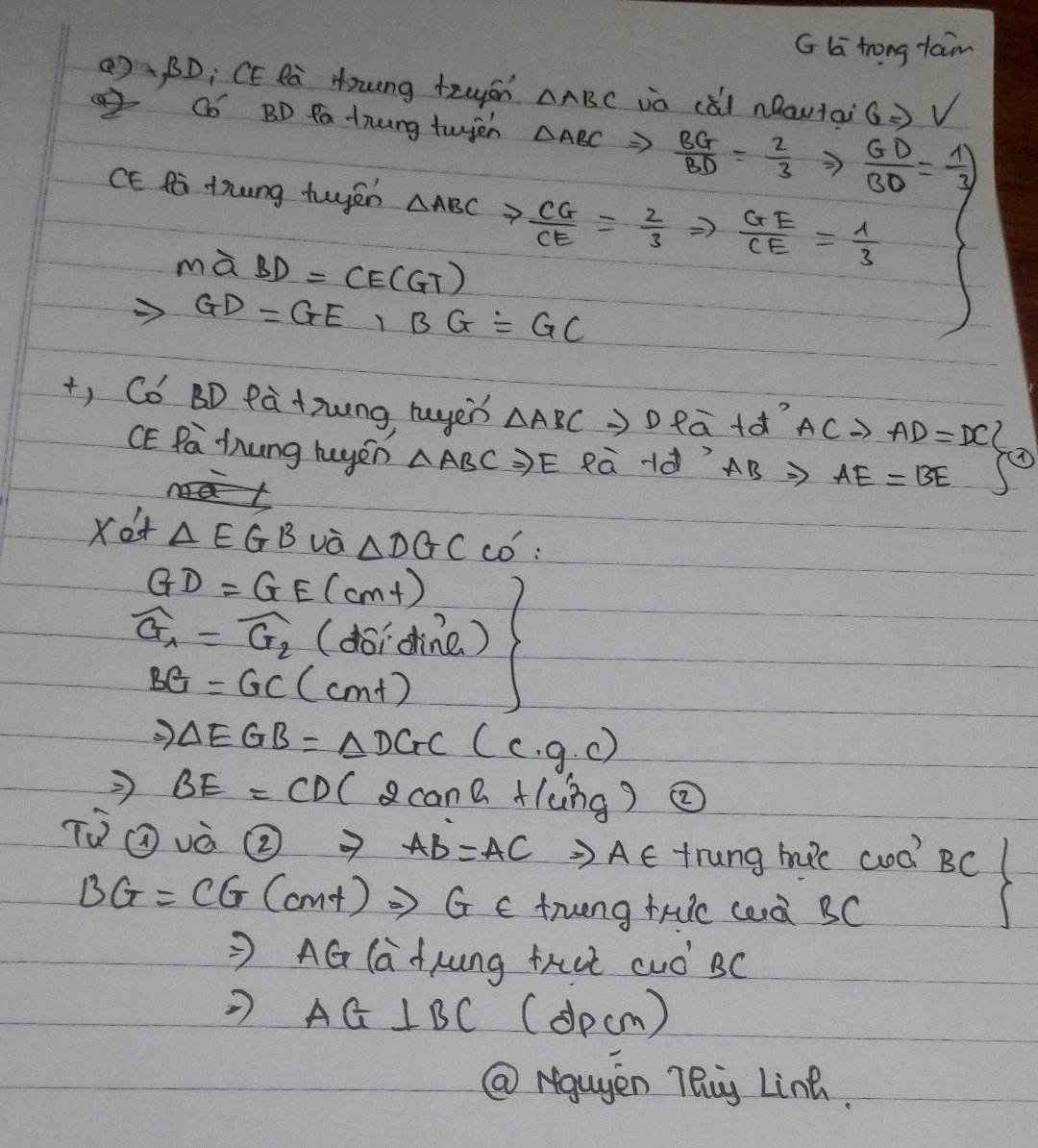
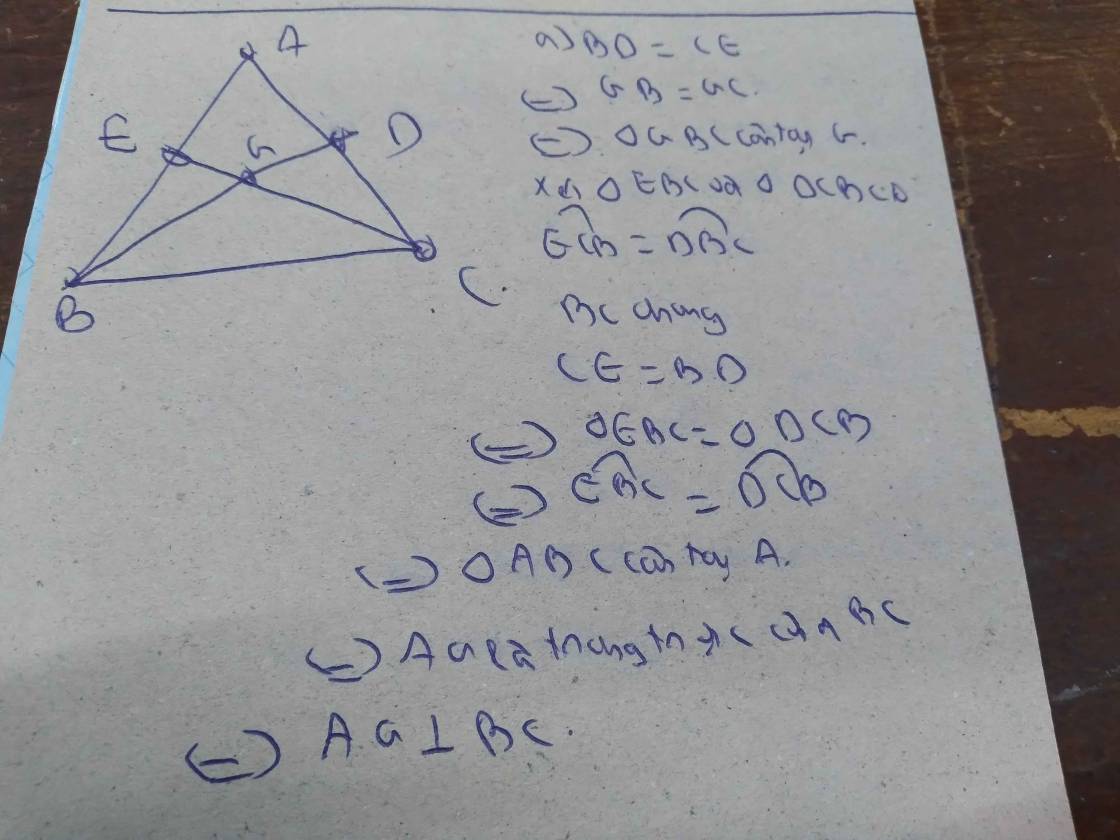
Ta có: giao điểm của 2 đường trung tuyến là trọng tâm △ABC
Áp dụng tính chất đường trung tuyến ta có:
\(3GE=2GC=CE;3GD=2GB=BD\)
Mà BD = CE \(\Rightarrow GD=GE;GC=GB\)
Xét △EGB và △DGC có:
GD = GE (cmt)
\(\hat{EGB}=\hat{DGC}\)
GC = CB (cmt)
\(\Rightarrow\triangle EGB=\triangle DGC\left(cgc\right)\Rightarrow BE=DC\)
Mà BD là đường trung tuyến \(\Rightarrow BE=EA=\frac{AB}{2}\)
CE là đường trung tuyến \(\Rightarrow DC=AD=\frac{AC}{2}\)
\(\Rightarrow AB=AC\) hay △ABC cân
b) Gọi giao điểm AG và BC là: Q
G là trọng tâm △ABC \(\Rightarrow\) \(BQ=QC\)
Xét △AQB và △AQC có:
BQ = QC (cmt)
AQ chung
AB = AC (cmt)
\(\Rightarrow\triangle AQB=\triangle AQC\left(ccc\right)\Rightarrow AQB=AQC\)
Hai góc kề bù
\(\Rightarrow AQB=AQC=\frac{180^{O}}{2}=90^{O}\) hay AQ ⊥BC