Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

- Chứng minh ∆ADE = ∆ABC:
Dùng tiêu chí Cạnh-Góc-Cạnh vì:- \(A B = A D\) (A là trung điểm của BD).
- \(A C = A E\) (A là trung điểm của CE).
- \(\angle B A C = \angle D A E\) (góc đối đỉnh).
- Chứng minh DE // BC:
Vì \(\Delta A D E = \Delta A B C\) (theo C-G-C), nên:
\(\angle A D E = \angle A B C\) và \(\angle D E A = \angle A C B\).
→ DE // BC theo định lý góc đồng vị. - Chứng minh M, A, N thẳng hàng:
M, N lần lượt là trung điểm của DE và BC nên AM là đường trung bình của tam giác lớn. Đường trung bình đi qua trung điểm nối song song với cạnh còn lại nên M, A, N thẳng hàng.

a: Gọi G là trọng tâm, M là trung điểm của BC
=>AG=2/3AM
BM+BE=EM
CM+CF=MF
mà BM=CM; BE=CF
nên EM=MF
=>M là trung điểm củaEF
Xet ΔAEF có
AM là trung tuyến
AG=2/3AM
=>G là trọng tâm của ΔAEF
b: G là trọng tâm cùa ΔAEF
=>N là trung điểm của AF
Xét ΔAEF có FM/FE=FN/FA
nên MN//AE và MN=1/2AE
Xét ΔGAE có GH/GA=GI/GE
nên HI//AE và HI=1/2AE
=>MN//HI và MN=HI

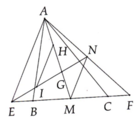


vẽ hình đi rồi giải cho
a: ΔABC có G là trọng tâm
nên AG cắt BC tại trung điểm M của BC
=>\(AG=\dfrac{2}{3}AM\)
Ta có: MB+BD=MD
MC+CE=ME
mà MB=MC và BD=CE
nên MD=ME
=>M là trung điểm của DE
Xét ΔADE có
AM là đường trung tuyến
\(AG=\dfrac{2}{3}AM\)
Do đó: G là trọng tâm của ΔDAE
b: Xét ΔDAE có
G là trọng tâm
=>N là trung điểm của AE
Xét ΔEAD có
M,N lần lượt là trung điểm của ED,EA
=>MN là đường trung bình của ΔEAD
=>MN//AD và MN=AD/2(1)
Xét ΔGAD có
I,J lần lượt là trung điểm của GA,GD
=>JI là đường trung bình của ΔEAD
=>JI//AD và JI=AD/2(2)
Từ (1),(2) suy ra MN//JI và MN=JI