Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

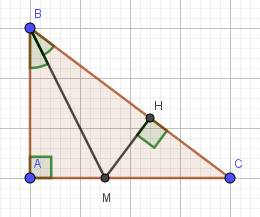
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)

nhớ tk cho ming nha
A C B M H N
1, Xét tam giác ABC có :
\(BC^2=AC^2+AB^2\)
\(\Leftrightarrow BC^2=4^2+3^2\)
\(\Leftrightarrow BC^2=25\)
\(\Leftrightarrow BC=5\left(cm\right)\)
2,Ta có :\(\widehat{BMA}+\widehat{MBA}=90^O\)
\(\widehat{BMH}+\widehat{MBH}=90^O\)
MÀ \(\widehat{ABM}=\widehat{HBM}\)
Nên \(\widehat{BMA}=\widehat{BMH}\)
Xét tam giác ABM và tam giác HBM có :
\(\widehat{ABM}=\widehat{HBM}\left(gt\right)\)
\(BMchung\)
\(\widehat{BMA}=\widehat{BMH}\)
\(\Rightarrow\Delta BAM=\Delta BHM\left(c.g.c\right)\)
3,Vì \(\Delta BAM=\Delta BHM\Rightarrow AM=MH\left(1\right)\)
Xét \(\Delta HMC\)có :
\(\widehat{MHC}=90^0\)
Suy ra :MC>MH(2)
Từ (1) và(2):AM<MC
4,Ta có :\(\widehat{AMH}+\widehat{HMC}=180^0\left(1\right)\)
Xét tam giác NMA và tam giác CMH có:
\(HC=NA\)
\(\widehat{NAM}=\widehat{CHM}\)
\(MA=MH\left(\Delta BAM=\Delta BHM\right)\)
\(\Rightarrow\Delta NMA=\Delta CMH\left(c.g.c\right)\)
\(\Rightarrow\widehat{NMA}=\widehat{CMH}\)(2)
Từ (1) và(2) : => N,M,H thẳng hàng

a) Xét ΔAMB vuông tại A và ΔHMB vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)(BM là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔAMB=ΔHMB(Cạnh huyền-góc nhọn)
Suy ra: AM=HM(Hai cạnh tương ứng)

A B C I M K
a, Xét tam giác vuông MHC có :
\(\widehat{CMH}+\widehat{HCM}=90^o\)
Xét tam giác vuông ABC có:
\(\widehat{HIB}+\widehat{HCM}=90^o\)
\(\Rightarrow\widehat{CMH}=\widehat{HIB}\)
Xét 2 tam giác : KHM và IHB
MH = HB ( gt )
\(\widehat{CMN}=\widehat{HBI}\left(cmt\right)\)
\(\widehat{MKH}=\widehat{HIB}=90^o\)
\(\Rightarrow\Delta KHM=\Delta IHB\)
b, \(\Rightarrow HK=HI\)
Xét 2 tam giác : KHA và IHA
KM = IH ( cm a )
AN chung
\(\widehat{HKA}=\widehat{AIM}=90^o\)
\(\Rightarrow\Delta KHA=\Delta IHA\)
\(\Rightarrow\widehat{KAH}=\widehat{HAI}\)
Vậy : AH là tia phân giác góc BAC
a, xet △ vuong mhc co ∠cmh + ∠hcm = 90 do xet △ vuong abc co ∠hbi + ∠hcm = 90 do suy ra ∠cmh = ∠hbi xet △ BHI va △ MHK co ∠CMH = ∠HBI [c/m tr] HM = BH [gt] ∠BIH = ∠MKH [=90 do] ➩ △ BHI = △ MHK [ch-gn] b, tu a co △bhi = △mhk ➩ ih = kh xet △aih va △akh co ah chung ih = kh [c/m tr] ∠aih = ∠akh [= 90 do] ➩ △aih = △kah [ch-cgv] ➩ ∠iah = ∠kah ➩ ah la p/g cua ∠bac
Để chứng minh \(A M < M C\) trong tam giác vuông \(A B C\), ta sẽ dùng các tính chất về tia phân giác và các đoạn thẳng vuông góc.
Dữ liệu bài toán:
Chứng minh:
\(\frac{A B}{B C} = \frac{A M}{M C}\)
Điều này có nghĩa là tỷ lệ giữa hai đoạn \(A B\) và \(B C\) sẽ bằng tỷ lệ giữa các đoạn \(A M\) và \(M C\).
\(A M < M C\)
Vậy ta đã chứng minh được rằng \(A M < M C\).
Xét ΔBAM vuông tại A và ΔBHM vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)
Do đó: ΔBAM=ΔBHM
=>MA=MH
mà MH<MC(ΔMHC vuông tại H)
nên MA<MC