NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
26 tháng 3 2016
a) Áp dụng bất đẳng thức Cauchy cho các số dương, ta có :
\(\log_23+\log_32>2\sqrt{\log_23.\log_32}=2\sqrt{1}=2\)
Không xảy ra dấu "=" vì \(\log_23\ne\log_32\)
Mặt khác, ta lại có :
\(\log_23+\log_32<\frac{5}{2}\Leftrightarrow\log_23+\frac{1}{\log_23}-\frac{5}{2}<0\)
\(\Leftrightarrow2\log^2_23-5\log_23+2<0\)
\(\Leftrightarrow\left(\log_23-1\right)\left(\log_23-2\right)<0\) (*)
Hơn nữa, \(2\log_23>2\log_22>1\) nên \(2\log_23-1>0\)
Mà \(\log_23<\log_24=2\Rightarrow\log_23-2<0\)
Từ đó suy ra (*) luôn đúng. Vậy \(2<\log_23+\log_32<\frac{5}{2}\)
b) Vì \(a,b\ge1\) nên \(\ln a,\ln b,\ln\frac{a+b}{2}\) không âm.
Áp dụng bất đẳng thức Cauchy ta có
\(\ln a+\ln b\ge2\sqrt{\ln a.\ln b}\)
Suy ra
\(2\left(\ln a+\ln b\right)\ge\ln a+\ln b+2\sqrt{\ln a\ln b}=\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
Mặt khác :
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\ln\frac{a+b}{2}\ge\frac{1}{2}\left(\ln a+\ln b\right)\)
Từ đó ta thu được :
\(\ln\frac{a+b}{2}\ge\frac{1}{4}\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
hay \(\frac{\sqrt{\ln a}+\sqrt{\ln b}}{2}\le\sqrt{\ln\frac{a+b}{2}}\)
c) Ta chứng minh bài toán tổng quát :
\(\log_n\left(n+1\right)>\log_{n+1}\left(n+2\right)\) với mọi n >1
Thật vậy,
\(\left(n+1\right)^2=n\left(n+2\right)+1>n\left(n+2\right)>1\)
suy ra :
\(\log_{\left(n+1\right)^2}n\left(n+2\right)<1\Leftrightarrow\frac{1}{2}\log_{n+1}n\left(n+2\right)<1\)
\(\Leftrightarrow\log_{n+1}n+\log_{\left(n+1\right)}n\left(n+2\right)<2\)
Áp dụng bất đẳng thức Cauchy ta có :
\(2>\log_{\left(n+1\right)}n+\log_{\left(n+1\right)}n\left(n+2\right)>2\sqrt{\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)}\)
Do đó ta có :
\(1>\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)\) và \(\log_n\left(n+1>\right)\log_{\left(n+1\right)}\left(n+2\right)\) với mọi n>1
5 tháng 5 2016
Ta xét 3 trường hợp :
* Nếu \(x>4\) thì \(x-3>1\Rightarrow\left(x-3\right)^{2010}>1\Rightarrow\left(x-3\right)^{2010}+\left(x+4\right)^{2012}>1\) mâu thuẫn.
* Nếu \(x< 3\) thì \(x-4< -1\Rightarrow\left(x-4\right)^{2010}>1\Rightarrow\left(x-3\right)^{2010}+\left(x+4\right)^{2012}>1\) mâu thuẫn.
* Nếu \(3< x< 4\) thì \(x-3>1\Rightarrow\left|x-3\right|,\left|x-4\right|\le1\Rightarrow\left(x-3\right)^{2010}< \left(x-3\right),\left(x-4\right)^{2012}\le\left(4-x\right)\)
Do đó \(\left(x-3\right)^{2010}+\left(x-4\right)^{2012}< \left(x-3\right)+\left(4-x\right)=1\) cũng mâu thuẫn
Mặt khác, với \(x=3;x=4\) thì đẳng thức đúng. Vậy ta có điều phải chứng minh
27 tháng 3 2016
Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)
Q
31 tháng 3 2017
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
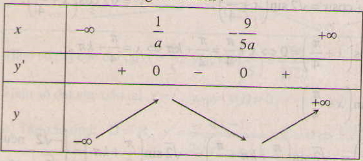
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
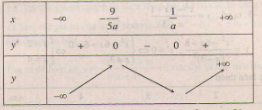
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
23 tháng 4 2016
Theo yêu cầu bài toán ta có \(\begin{cases}ab< 0\\AB=BC=CA\end{cases}\) \(\Leftrightarrow\begin{cases}m< 2\\8\left(m-2\right)^3+24=0\end{cases}\)
\(\Leftrightarrow m=2-\sqrt[3]{3}\)
JN
8 tháng 1 2022
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [–π2;3π2][–π2;3π2] và các hàm số y = |x| trên khoảng (-∞; +∞).
Q
31 tháng 3 2017
*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2018
\(log\left(5\left(x^2+1\right)\right)\ge log\left(mx^2+4x+m\right)\)
- BPT đúng \(\forall x\Rightarrow log\left(mx^2+4x+m\right)\) xác định \(\forall x\in R\)
\(\Rightarrow mx^2+4x+m>0\) \(\forall x\in R\)
\(\Rightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=4-m^2< 0\end{matrix}\right.\) \(\Rightarrow m>2\) (1)
- Lại có \(x^2+1\ge1\) \(\forall x\)
\(\Rightarrow5\left(x^2+1\right)\ge mx^2+4x+m\)
\(\Leftrightarrow5\left(x^2+1\right)-4x\ge m\left(x^2+1\right)\)
\(\Leftrightarrow5-\dfrac{4x}{x^2+1}\ge m\)
Đặt \(f\left(x\right)=5-\dfrac{4x}{x^2+1}\Rightarrow f\left(x\right)\ge m\) \(\forall x\Leftrightarrow m\le min\left(f\left(x\right)\right)\)
Ta có \(f\left(x\right)=3+2-\dfrac{4x}{x^2+1}=3+\dfrac{2\left(x-1\right)^2}{x^2+1}\ge3\)
\(\Rightarrow min\left(f\left(x\right)\right)=3\Rightarrow m\le3\) (2)
Kết hợp (1), (2) \(\Rightarrow2< m\le3\Rightarrow m=3\)
Vậy có 1 giá trị nguyên duy nhất của m để BPT đúng với mọi x
Đáp án B
(5+5+5+5)x5=100