Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1. Điền kí hiệu ( ∈,⊂, ∉) thích hợp vào ô vuông
– 3 ∉ N – 3 ∈ Z -3 ∈ Q
-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q
Bài 2 trang 7. Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ 3/-4

bài 3
hD Giải: a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
b)![]() Vì -216 < -213 và 300 > 0 nên y < x
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x=y
Bài 4. So sánh số hữu tỉ a/b ( a,b ∈ Z, b # 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu
HD giải: Với a, b ∈ Z, b> 0
– Khi a , b cùng dấu thì a/b > 0
– Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{x-2y+3z-1+4-9}{2-2\cdot3+3\cdot4}=1\)
Do đó: x=3; y=5; z=7

Bài 4:
Gọi 3 số là a,b,c
Ta có \(a:b=2:3\Rightarrow\dfrac{a}{2}=\dfrac{b}{3};a:c=4:9\Rightarrow\dfrac{a}{4}=\dfrac{c}{9}\)
\(\Rightarrow\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{9}\Rightarrow\dfrac{a^3}{64}=\dfrac{b^3}{216}=\dfrac{c^3}{729}\) và \(a^3+b^3+c^3=-1009\)
Áp dụng t/c dtsbn:
\(\dfrac{a^3}{64}=\dfrac{b^3}{216}=\dfrac{c^3}{729}=\dfrac{a^3+b^3+c^3}{64+216+729}=\dfrac{-1009}{1009}=-1\\ \Rightarrow\left\{{}\begin{matrix}a^3=-64\\b^3=-216\\c^3=-729\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-4\\b=-6\\c=-9\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số sách tủ 1,2,3 trước khi chuyển là là a,b,c (cuốn;a,b,c∈N*)
Ta có \(\left(a-100\right):b:\left(c+100\right)=16:15:14\Rightarrow\dfrac{a-100}{16}=\dfrac{b}{15}=\dfrac{c+100}{14}\)
Và \(a+b+c=2250\)
Áp dụng t.c dstbn:
\(\dfrac{a-100}{16}=\dfrac{b}{15}=\dfrac{c+100}{14}=\dfrac{a-100+b+c+100}{16+15+14}=\dfrac{2250}{45}=50\\ \Rightarrow\left\{{}\begin{matrix}a-100=800\\b=750\\c+100=700\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=900\\b=750\\c=600\end{matrix}\right.\)
Vậy...

mik chưa có đề ôn tập hk2 nhưng mik có các bt hình hok lp 7 nè,bn muốn tham khảo ko?

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là các góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔBAK=ΔBHK
c: Ta có: ΔBAK=ΔBHK
=>KA=KH
Xét ΔKAI vuông tại A và ΔKHC vuông tại H có
KA=KH
AI=HC
Do đó: ΔKAI=ΔKHC
=>\(\widehat{AKI}=\widehat{HKC}\)
mà \(\widehat{HKC}+\widehat{AKH}=180^0\)(hai góc kề bù)
nên \(\widehat{AKH}+\widehat{AKI}=180^0\)
=>H,K,I thẳng hàng
d: Xét ΔBIC có \(\dfrac{BA}{AI}=\dfrac{BH}{HC}\)
nên AH//IC

Ta có P(x)=x^2+2x+x+2+3
=x(2+x)+x+2+3
=(x+2)^2+3
Mà (x+2)^2>=0=>P(x)>0
=> P(x) vô nghiệm

69 ) a) 8,5:3 = 2,8333... = 2,8(3)
b) 18,7 : 6 = 3,11666... = 3,11(6)
c) 58:11 = 5,272727... = 5,(27)
d) 14,2 : 3,33 = 4,264264264... = 4,(264)


A B C D M 1 2 1
trên tia đối của tia MA lấy điểm D sao cho MD = MA
xét \(\Delta AMB\)và \(\Delta DMC\)có :
MB = MC ( gt )
\(\widehat{M_1}=\widehat{M_2}\)( hai góc đối đỉnh )
MA = MD ( do cách vẽ )
Suy ra : \(\Delta AMB\)= \(\Delta DMC\)( c.g.c )
Suy ra : AB = AC và \(\widehat{A_1}=\widehat{D}\) \(\Rightarrow\)AB // CD ( vì có cặp góc sole trong bằng nhau )
vì \(AC\perp AB\)( gt ) nên AC \(\perp\)CD ( quan hệ giữa tính song song và vuông góc )
Xét \(\Delta ABC\)và \(\Delta CDA\)có :
AB = CD ( chứng minh trên )
\(\widehat{A}=\widehat{C}=90^o\)
AC ( chung )
Vậy \(\Delta ABC\)= \(\Delta CDA\)( c.g.c ) suy ra BC = AD
vì \(AM=MD=\frac{AD}{2}\)nên \(AM=\frac{BC}{2}\)
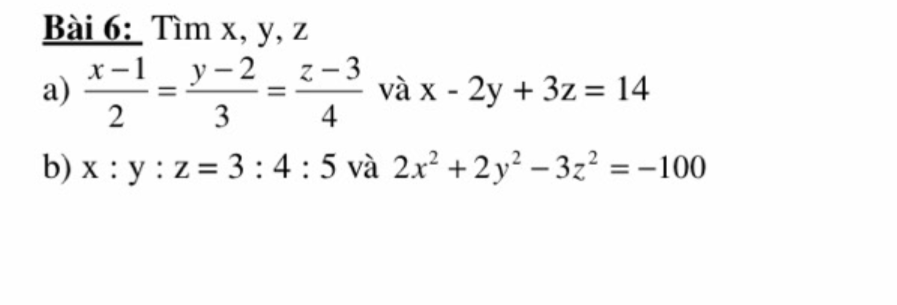

 NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!
NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!
bài nào ?