Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

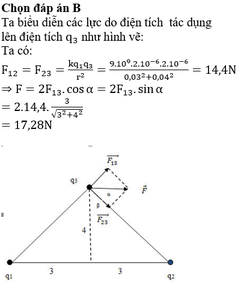
Chọn đáp án B
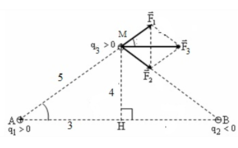
Ta biểu diễn các lực do điện tích tác dụng lên điện tích q 3 như hình vẽ:
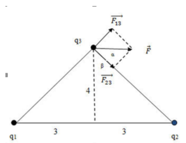
Ta có:
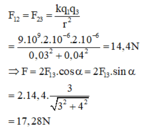

Ta có AM = BM = A H 2 + H M 2 = 12 2 + 16 2 = 20 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .9.10 − 6 0 , 2 2 = 20 , 25 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ.
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 A H A M = 2 . 20 , 25 . 10 5 12 20 = 24 , 3 . 10 5 (V/m).
F → = q 3 E → ; vì q 3 < 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 E = 5 . 10 - 8 . 24 , 3 . 10 5 = 0 , 1215 (N).

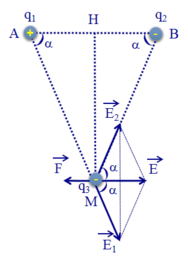
Ta có AM = BM = A H 2 + H M 2 = 9 2 + 12 2 = 15 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .6.10 − 6 0 , 15 2 = 24 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ, có độ lớn:
E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 . H M A M = 2 . 24 . 10 5 . 12 15 = 38 , 4 . 10 5 (V/m).
F → = q 3 . E → ; vì q 3 > 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 . E = 5 . 10 - 8 . 38 , 4 . 10 5 = 0 , 192 ( N )
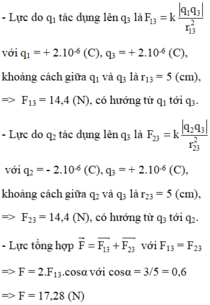

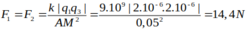
Để giải quyết các bài toán này, ta sẽ sử dụng công thức tính lực điện giữa hai điện tích:
\(F = k \cdot \frac{\mid q_{1} \cdot q_{2} \mid}{r^{2}}\)
Trong đó:
Thông số đã cho:
a) \(q_{3}\) đặt tại điểm C tạo thành một tam giác đều ABC
Trong trường hợp này, các điểm \(A\), \(B\), và \(C\) tạo thành một tam giác đều, vì vậy khoảng cách giữa \(C\) và \(A\), cũng như giữa \(C\) và \(B\), đều là \(r = 0.08 \textrm{ } \text{m}\).
Lực điện tác dụng lên \(q_{3}\) do \(q_{1}\) và \(q_{2}\):
\(F_{1} = k \cdot \frac{\mid q_{1} \cdot q_{3} \mid}{r^{2}} = 9 \times 10^{9} \times \frac{6 \times 10^{- 6} \times 4 \times 10^{- 6}}{\left(\right. 0.08 \left.\right)^{2}}\) \(F_{1} = 9 \times 10^{9} \times \frac{24 \times 10^{- 12}}{0.0064} \approx 3.375 \textrm{ } \text{N}\)
\(F_{2} = F_{1} \approx 3.375 \textrm{ } \text{N}\)
Phân tích vectơ lực:
Công thức tính tổng lực khi có góc \(\theta\) giữa hai vectơ lực:
\(F_{\text{t}ổ\text{ng}} = \sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} cos \theta}\)
Với \(\theta = 60^{\circ}\), ta có:
\(F_{\text{t}ổ\text{ng}} = \sqrt{\left(\right. 3.375 \left.\right)^{2} + \left(\right. 3.375 \left.\right)^{2} + 2 \cdot 3.375 \cdot 3.375 \cdot cos 60^{\circ}}\) \(F_{\text{t}ổ\text{ng}} = \sqrt{11.390625 + 11.390625 + 22.53125} = \sqrt{45.3125} \approx 6.73 \textrm{ } \text{N}\)
b) \(q_{3}\) đặt trên đường trung trực của \(A B\), cách đoạn \(A B\) một khoảng 3 cm
Khi \(q_{3}\) đặt trên đường trung trực của \(A B\), khoảng cách từ \(q_{3}\) đến \(A\) và \(q_{3}\) đến \(B\) đều bằng nhau, và bằng \(r = 0.03 \textrm{ } \text{m}\).
Lực điện tác dụng lên \(q_{3}\):
\(F_{1} = k \cdot \frac{\mid q_{1} \cdot q_{3} \mid}{r^{2}} = 9 \times 10^{9} \times \frac{6 \times 10^{- 6} \times 4 \times 10^{- 6}}{\left(\right. 0.03 \left.\right)^{2}}\) \(F_{1} = 9 \times 10^{9} \times \frac{24 \times 10^{- 12}}{0.0009} = 240 \textrm{ } \text{N}\)
\(F_{2} = 240 \textrm{ } \text{N}\)
Phân tích vectơ lực:
\(F_{\text{t}ổ\text{ng}} = F_{1} - F_{2} = 240 - 240 = 0 \textrm{ } \text{N}\)
Vậy lực tổng cộng tác dụng lên \(q_{3}\) là 0 N.
c) \(q_{3}\) đặt tại điểm C tạo thành một tam giác đều ABC đồng thời thay đổi dấu điện tích \(q_{2}\)
Trong trường hợp này, vì \(q_{2}\) có dấu âm, lực điện do \(q_{2}\) tác dụng lên \(q_{3}\) sẽ có hướng ngược lại so với khi \(q_{2}\) là dương. Tuy nhiên, độ lớn của các lực vẫn không thay đổi. Các phân tích vectơ lực tương tự như trong trường hợp a), chỉ khác là các vectơ lực từ \(q_{1}\) và \(q_{2}\) sẽ có hướng đối ngược.
Kết quả:
Vì lực tổng hợp vẫn là sự cộng của hai vectơ lực, nhưng chúng có hướng ngược lại, ta tính lại lực tổng hợp tương tự như trong phần a) và kết quả cuối cùng vẫn giữ nguyên.
Xem thử nha