Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

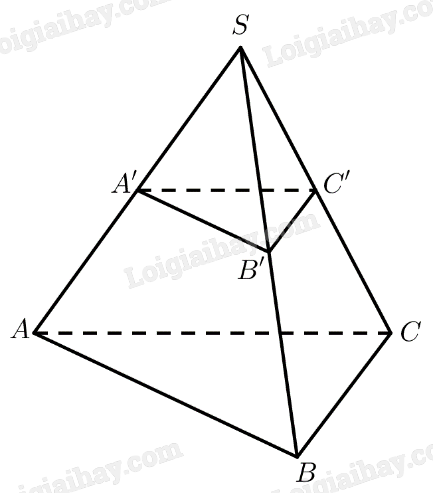
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của \(\Delta SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(\left. \begin{array}{l}A'B'\parallel \left( {ABC} \right)\\A'C'\parallel \left( {ABC} \right)\\A'B',A'C' \subset \left( {A'B'C'} \right)\end{array} \right\} \Rightarrow \left( {A'B'C'} \right)\parallel \left( {ABC} \right)\)
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.

Đáp án A
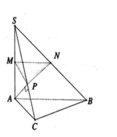
Xét tam giác SAC vuông tại A có AP là đường cao, ta có:
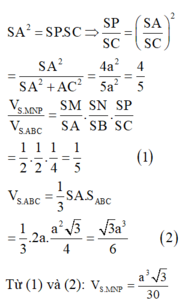

a) Tam giác đều ABC có diện tích \(S = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Tam giác đều A'B'C' có diện tích \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối chóp cụt
\(V = \frac{1}{3}.HH'.\left( {S + S' + \sqrt {S.S'} } \right) = \frac{1}{3}.h.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right) = \frac{{7{a^2}\sqrt 3 }}{{12}}\)
b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C')
Mà \(\left( {A{B_1}{C_1}} \right) \subset \left( {ABC} \right) \Rightarrow \left( {A{B_1}{C_1}} \right)//\left( {A'B'C'} \right)\)
Xét tam giác ABC có
B1,C1 tương ứng là trung điểm của AB, AC
\( \Rightarrow \) B1C1 là đường trung bình của tam giác ABC
\( \Rightarrow \) \({B_1}{C_1} = \frac{{BC}}{2}\) và B1C1 // BC mà \(B'C' = \frac{{BC}}{2}\) và BC // B’C’
\( \Rightarrow \) B1C1 = B’C’ và B1C1 // B’C’ \( \Rightarrow \) C1C’B’B1 là hình bình hành
Ta có \(A{B_1} = A'B' = \frac{{AB}}{2},A{B_1}//A'B'\) \( \Rightarrow \) AA’B’B1 là hình bình hành.
\(A{C_1} = A'C' = \frac{{AC}}{2},A{C_1}//A'C'\) \( \Rightarrow \) AA’C’C1 là hình bình hành.
Do đó AB1C1.A'B'C' là một hình lăng trụ
Thể tích hình lăng trụ \(V = HH'.S' = h.\frac{{{a^2}\sqrt 3 }}{4}\)

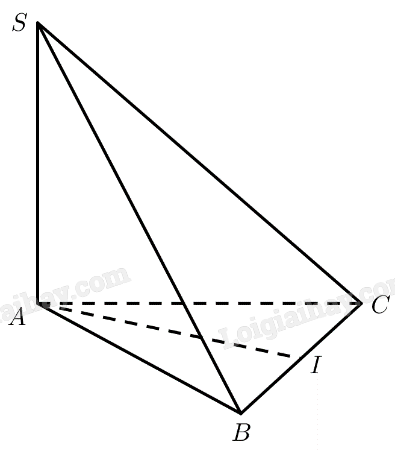
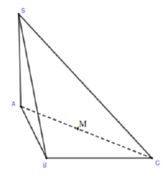
Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AI\)
\( \Rightarrow d\left( {SA,BC} \right) = AI = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
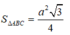
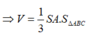






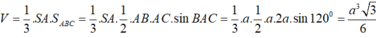
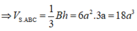
Bài giải
Bước 1: Xác định tỉ số đồng dạng
Vì \(A^{'} B^{'} C^{'}\) song song với \(A B C\) và hình chóp \(S . A B C\) là hình chóp đều, nên hai hình chóp \(S . A B C\) và \(S . A^{'} B^{'} C^{'}\) đồng dạng.
Theo đề bài, ta có tỉ số chiều cao:
\(\frac{S A^{'}}{S A} = \frac{2}{3}\)
\(\Rightarrow\) Tỉ số đồng dạng của hai hình chóp là:
\(k = \frac{S A^{'}}{S A} = \frac{2}{3}\)
Bước 2: Tính chiều cao của hình chóp \(S . A^{'} B^{'} C^{'}\)
Vì \(S A = 10\) cm nên:
\(S A^{'} = \frac{2}{3} \times 10 = \frac{20}{3} \&\text{nbsp};\text{cm}\)
Bước 3: Tính độ dài cạnh của đáy nhỏ \(A^{'} B^{'}\)
Do hai tam giác \(\triangle S A^{'} B^{'} sim \triangle S A B\) theo tỉ số đồng dạng \(k = \frac{2}{3}\), nên cạnh của đáy nhỏ là:
\(A^{'} B^{'} = \frac{2}{3} \times A B = \frac{2}{3} \times 6 = 4 \&\text{nbsp};\text{cm}\)
Bước 4: Tính thể tích của hai hình chóp
Thể tích của hình chóp được tính theo công thức:
\(V = \frac{1}{3} \times S_{đ \overset{ˊ}{\text{a}} \text{y}} \times h\)
Tính thể tích của hình chóp lớn \(S . A B C\)
Diện tích đáy \(A B C\) (là tam giác đều cạnh 6 cm):
\(S_{A B C} = \frac{\sqrt{3}}{4} \times 6^{2} = \frac{\sqrt{3}}{4} \times 36 = 9 \sqrt{3} \&\text{nbsp};\text{cm}^{2}\)
Thể tích của hình chóp \(S . A B C\):
\(V_{S . A B C} = \frac{1}{3} \times 9 \sqrt{3} \times 10 = 30 \sqrt{3} \&\text{nbsp};\text{cm}^{3}\)
Tính thể tích của hình chóp nhỏ \(S . A^{'} B^{'} C^{'}\)
Diện tích đáy \(A^{'} B^{'} C^{'}\) (tam giác đều cạnh 4 cm):
\(S_{A^{'} B^{'} C^{'}} = \frac{\sqrt{3}}{4} \times 4^{2} = \frac{\sqrt{3}}{4} \times 16 = 4 \sqrt{3} \&\text{nbsp};\text{cm}^{2}\)
Thể tích của hình chóp nhỏ \(S . A^{'} B^{'} C^{'}\):
\(V_{S . A^{'} B^{'} C^{'}} = \frac{1}{3} \times 4 \sqrt{3} \times \frac{20}{3} = \frac{80 \sqrt{3}}{9} \&\text{nbsp};\text{cm}^{3}\)
Bước 5: Tính thể tích hình chóp cụt
Thể tích hình chóp cụt \(A^{'} B^{'} C^{'} . A B C\) là hiệu hai thể tích:
\(V_{\text{ch} \overset{ˊ}{\text{o}} \text{p}\&\text{nbsp};\text{c}ụ\text{t}} = V_{S . A B C} - V_{S . A^{'} B^{'} C^{'}}\) \(V_{\text{ch} \overset{ˊ}{\text{o}} \text{p}\&\text{nbsp};\text{c}ụ\text{t}} = 30 \sqrt{3} - \frac{80 \sqrt{3}}{9}\)
Quy đồng:
\(V_{\text{ch} \overset{ˊ}{\text{o}} \text{p}\&\text{nbsp};\text{c}ụ\text{t}} = \frac{270 \sqrt{3}}{9} - \frac{80 \sqrt{3}}{9} = \frac{190 \sqrt{3}}{9} \approx 36.63 \&\text{nbsp};\text{cm}^{3}\)
Đáp số: \(\frac{190 \sqrt{3}}{9}\) cm³ (khoảng 36,63 cm³)
Bài giải
Bước 1: Xác định tỉ số giữa hai mặt phẳng đáy
Do \(A^{'} B^{'} C^{'} \parallel A B C\) và \(S A^{'} / S A = \frac{2}{3}\), ta suy ra:
\(\frac{A^{'} B^{'}}{A B} = \frac{S A^{'}}{S A} = \frac{2}{3}\)
Vậy độ dài cạnh của \(A^{'} B^{'} C^{'}\) là:
\(A^{'} B^{'} = A B \times \frac{2}{3} = 6 \times \frac{2}{3} = 4 \&\text{nbsp};\text{cm}\)
Bước 2: Xác định chiều cao của hình chóp \(S . A B C\) và \(S . A^{'} B^{'} C^{'}\)
Bước 3: Tính thể tích hai hình chóp
Thể tích hình chóp được tính theo công thức:
\(V = \frac{1}{3} B h\)
Trong đó:
Thể tích hình chóp \(S . A B C\):
Diện tích đáy \(A B C\) (là tam giác đều) được tính theo công thức:
\(B = \frac{\sqrt{3}}{4} a^{2} = \frac{\sqrt{3}}{4} \left(\right. 6^{2} \left.\right) = \frac{\sqrt{3}}{4} \times 36 = 9 \sqrt{3} \&\text{nbsp};\text{cm}^{2}\)
Thể tích của hình chóp \(S . A B C\) là:
\(V_{S . A B C} = \frac{1}{3} \times 9 \sqrt{3} \times 10 = 30 \sqrt{3} \&\text{nbsp};\text{cm}^{3}\)
Thể tích hình chóp \(S . A^{'} B^{'} C^{'}\):
Tương tự, diện tích đáy \(A^{'} B^{'} C^{'}\) là:
\(B^{'} = \frac{\sqrt{3}}{4} \left(\right. 4^{2} \left.\right) = \frac{\sqrt{3}}{4} \times 16 = 4 \sqrt{3} \&\text{nbsp};\text{cm}^{2}\)
Thể tích của hình chóp \(S . A^{'} B^{'} C^{'}\) là:
\(V_{S . A^{'} B^{'} C^{'}} = \frac{1}{3} \times 4 \sqrt{3} \times 6 , 7 = 8 , 93 \sqrt{3} \&\text{nbsp};\text{cm}^{3}\)
Bước 4: Tính thể tích hình chóp cụt \(A^{'} B^{'} C^{'} . A B C\)
\(V_{\text{ch} \overset{ˊ}{\text{o}} \text{p}\&\text{nbsp};\text{c}ụ\text{t}} = V_{S . A B C} - V_{S . A^{'} B^{'} C^{'}}\) \(= 30 \sqrt{3} - 8 , 93 \sqrt{3} = 21 , 07 \sqrt{3} \&\text{nbsp};\text{cm}^{3}\)
Đáp số: \(V \approx 36 , 5\) cm³ (làm tròn đến 1 chữ số thập phân)