Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N H E D I I
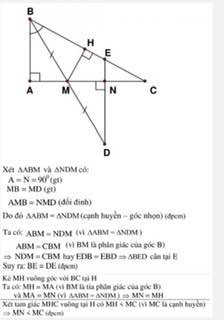
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay MB=MC

a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC

a) c/m tam giác BMI =CMI (c. g. c)
=>BM=CM(hai cạnh tương ứng)
Xét tam giác BMC có BM=CM (cmt)
=> tam giác BMC cân tại M
b) Xét tam giác ABC có
Góc BAC + gócABC+ góc ACB =180 độ
=>góc ABC=60 độ
Ta lại cos tam giác BMC cân tại M =>gocs MBC=góc C =30 độ
Mà góc ABC =ABM+CBM
=>CBM=ABM=30 độ =1/2ABC
Vậy BM là phân giác của góc ABC
c) c/m tam giác ABM= tam giác ibm( cạnh huyền canh góc vuông)
=> AB=BI
MÀ BI=1/2BC=>AB=1/2BC
d) c/m tam giác BKI=BCA( c. g. c)
=> góc KIB=góc CAB=90 độ
=> KI vuông góc với BC
mà MI cũng vuoong góc với BC
=>3 điểm K,M,I thẳng hàng

Bạn tự vẽ hình nhé.
a) Xét tam giác \(ABM\)và tam giác \(NBM\)có:
\(\widehat{MAB}=\widehat{MNB}\left(=90^o\right)\)
\(MB\)cạnh chung
\(\widehat{MBA}=\widehat{MBN}\)(vì \(BM\)là tia phân giác \(\widehat{ABN}\))
suy ra \(\Delta ABM=\Delta NBM\)(cạnh huyền - góc nhọn)
\(\Rightarrow\widehat{AMB}=\widehat{NMB}\)(Hai góc tương ứng)
suy ra \(MB\)là tia phân giác góc \(AMN\).
b) Vì \(NK//BM\)nên \(\widehat{BMN}=\widehat{MNK}\)(hai góc so le trong)
và \(\widehat{BMA}=\widehat{NKM}\)(Hai góc đồng vị)
mà \(\widehat{AMB}=\widehat{NMB}\)(theo a))
suy ra \(\widehat{MNK}=\widehat{NKM}\)suy ra tam giác \(MNK\)cân tại \(M\).
c) Vì \(\Delta ABM=\Delta NBM\)nên
+) \(MN=MA\)(Hai cạnh tương ứng) suy ra \(M\)thuộc đường trung trực của \(AN\).
+) \(BN=BA\)(Hai cạnh tương ứng) suy ra \(B\)thuộc đường trung trực của \(AN\).
suy ra \(BM\)là đường trung trực của \(AN\)\(\Rightarrow BM\perp AN\).
mà \(NK//BM\)suy ra \(AN\perp NK\).
Trong tam giác vuông \(ANK\): \(AN< AK\)(cạnh góc huyền lớn hơn cạnh góc vuông).
d) \(K\)là trung điểm \(MC\)suy ra \(MK=\frac{1}{2}MC\)mà \(MN=MK\)(do tam giác \(MNK\)cân tại \(M\))
suy ra \(MN=\frac{1}{2}MC\).
Trong tam giác vuông, cạnh góc vuông bằng \(\frac{1}{2}\)cạnh huyền thì góc đối diện với cạnh góc vuông đó bằng \(30^o\).
Do đó \(\widehat{C}=30^o\).
Vậy tam giác vuông \(ABC\)cần thêm điều kiện \(\widehat{C}=30^o\).

Câu a: Chứng minh tam giác ABH = tam giác ACH
Ta có tam giác ABC cân tại A, tức là ( AB = AC ).
Điểm ( H ) là trung điểm của đoạn ( BC ), nên ( BH = HC ).
Xét hai tam giác ( ABH ) và ( ACH ):
- ( AB = AC ) (giả thiết tam giác ABC cân tại A).
- ( BH = HC ) (do ( H ) là trung điểm của ( BC )).
- ( \angle ABH = \angle ACH ) (đối đỉnh).
Vậy theo cạnh - góc - cạnh (c.g.c), ta có:
[ \triangle ABH = \triangle ACH ]
Câu b: Chứng minh ( \angle ABM = \angle ACM ) và tam giác MBC cân
- Vì ( M ) nằm trên tia phân giác của góc ( ABC ), ta có: [ \angle ABM = \angle CBM ]
- Mặt khác, do tam giác ( ABH ) và ( ACH ) bằng nhau (chứng minh ở câu a), nên: [ \angle CBM = \angle ACM ] Suy ra:
[ \angle ABM = \angle ACM ] - Xét tam giác ( MBC ):
- ( \angle CBM = \angle BCM ) (do ( M ) nằm trên tia phân giác của ( \angle ABC )).
- ( MB = MC ) (cạnh đối diện hai góc bằng nhau).
Vậy tam giác ( MBC ) cân tại ( M ).
Câu c: Chứng minh ( AB = AN )
- Do đường thẳng đi qua ( A ) song song với ( BC ) cắt tia ( BM ) tại ( N ), ta có:
[ AN \parallel BC ] - Xét tam giác ( ABN ), có ( AN \parallel BC ) nên theo định lý đường trung bình của tam giác, ta có:
[ AB = AN ]
Câu d: Chứng minh ( MC \perp CN )
- Từ câu b, tam giác ( MBC ) cân tại ( M ) nên ( MC = MB ).
- Do ( AN \parallel BC ), nên góc ( MCN ) bằng góc ( NBC ).
- Mà ( \angle NBC = 90^\circ ) (do đường thẳng ( AN ) song song với ( BC )).
- Vậy suy ra ( MC \perp CN ).
Xét ΔABC có \(\widehat{BAC}+\widehat{BCA}+\widehat{ABC}=180^0\)
=>\(\widehat{ACB}=180^0-30^0-50^0=100^0\)
CM là phân giác của góc ACB
=>\(\widehat{ACM}=\widehat{BCM}=\dfrac{\widehat{ACB}}{2}=\dfrac{100^0}{2}=50^0\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\left(=50^0\right)\)
nên ΔMBC cân tại M
=>MB=MC
U