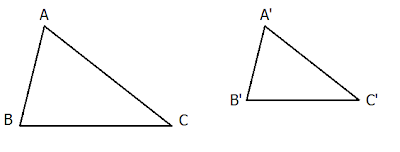
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhau
ABA′B′=BCB′C′=CAC′A′
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 2 2019
- Có
- Các trường hợp là :
đồng dạng (c.c.c) , đồng dạng (g.g) , đông dạng (c.g.c)
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
Ba cặp cạnh tỉ lệ với nhau
4 tháng 2 2019
đồng dạng (c.c.c) , đồng dạng (g.g) , đồng dạng (c.g.c)
Tam giác đồng dạng có hai tính chất quan trọng sau đây:
∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhau
ABA′B′=BCB′C′=CAC′A′
Vậy làm thế nào để chứng minh hai tam giác là đồng dạng với nhau. Thông thường chúng ta có ba cách sau đây.
Trường hợp Góc - Góc: hai tam giác có hai cặp góc bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
∠A=∠A′ và ∠B=∠B′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Cạnh - Cạnh: hai tam giác có ba cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
ABA′B′=BCB′C′=CAC′A′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Góc - Cạnh: hai tam giác có hai cặp cạnh tỉ lệ với nhau và cặp góc xen giữa hai cặp cạnh này bằng nhau thì đó là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
ABA′B′= BCB′C′ và ∠B=∠B′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.
- Nếu hai tam giác là hai tam giác vuông thì việc chứng minh hai tam giác là đồng dạng còn đơn giản hơn nữa. Chúng ta có các cách sau đây.
Trường hợp Góc Nhọn: hai tam giác vuông có một cặp góc nhọn bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được
∠A=∠A′
thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.
Trường hợp Cạnh - Cạnh: hai tam giác vuông có hai cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình trên đây, nếu chúng ta chỉ ra được
ABA′B′= BCB′C′, hoặc BCB′C′= CAC′A′, hoặc CAC′A′= ABA′B′
thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.
14 tháng 5 2017
a) - Xét hai tam giác vuông AHC và DFC có:
Góc C chung
Suy ra: tam giác AHC đồng dạng với tam giác DFC
b) - Xét hai tam giác vuông AHB và DEB có:
Góc B chung
suy ra: tam giác AHB đồng dạng với tam giác DEB
suy ra: AH/DE = AB/DB suy ra: AH.DB=DE.AB (đfcm)
c) xét hai tam giác DEF và ACB có :
góc E = góc C (= góc EDB)
góc F = góc B (= góc FDC)
suy ra : tam giác DEF = tam giác ACB (g.g)
suy ra: DE/DF = AC/AB
4 tháng 5 2019
Bạn tự vẽ hình nhé :^
a) Xét tam giác ABD và tam giác ACE có :
góc ADB = góc ACE ( vì cùng bằng 90 độ )
góc BAC chung
=> tam giác ABD đồng dạng với tam giác ACE ( g.g)
b) Vì tam giác ABD đồng dạng với tam giác ACE (cmt)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\)( định nghĩa tam giác đồng dạng)
Xét tam giác ADE và tam giác ABC có
\(\frac{AD}{AE}=\frac{AB}{AC}\)(cmt)
\(\widehat{BAC}\)chung
\(\Rightarrow\) tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
Còn câu c là gì vậy ạ ?
4 tháng 2 2017
Cho a',b',c' là số đo cạnh của tam giác A'B'C'
a,b,c là số đo cạnh của tam giác ABC
a) Theo đề bài ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=k=\frac{3}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=\frac{a'+b'+c'}{a+b+c}=\frac{P_{A'B'C'}}{P_{ABC}}=k=\frac{3}{5}\)
Vậy tỉ số chu vi hai tam giác đã cho là 3/5
b) Chu vi tam giác ABC là: \(P_{ABC}=40:\left(5-3\right)\cdot5=100\left(dm\right)\)
Chu vi tam giác A'B'C' là: \(P_{A'B'C'}=P_{ABC}-40dm=100dm-40dm=60\left(dm\right)\)
HH
19 tháng 4 2020
A B C A' B' C'
a, Gọi CV tam giác A'B'C' là P', ABC là P
\(\Delta A'B'C'~\Delta ABC\)theo tỉ số đồng dạng \(k=\frac{3}{5}\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=\frac{3}{5}\)
Áp dụng t/c DTSBN , ta có :
\(\frac{3}{5}=\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(=\frac{A'B'+B'C'+C'A'}{AB+BC+CA}=\frac{P'}{P}\)
Vậy tỉ số chu vi tam giác A'B'C' và ABC là \(\frac{3}{5}\)
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng giạng với tam giác đã cho