K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
24 tháng 2 2019
Đáp án A
![]()
![]()
Theo định lí 3 đường vuông góc, ta có
![]()
![]()
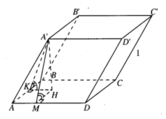
Ta cũng có HKAM là hình chữ nhật, đặt A'H = h ta có
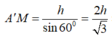
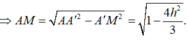
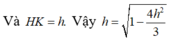
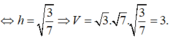
NK
1

6 tháng 2 2021
Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

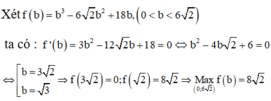

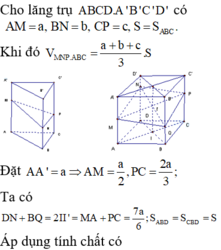
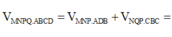
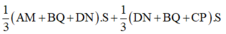
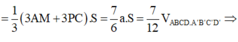
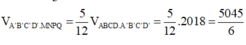


Gọi cạnh đáy hình vuông là x.
Áp dụng định lý Pitago cho tam giác ABC vuông tại B, ta có: AC² = AB² + BC² (2√3a)² = x² + x² 12a² = 2x² x² = 6a² x = a√6 Gọi O là giao điểm của AC và BD. Góc nhị diện [C', BD, C] là góc giữa đường thẳng C'O và mặt phẳng (ABCD).
Kẻ C'H vuông góc với BD tại H. Khi đó góc C'OH = 60°. Trong tam giác vuông COD, ta có: OC = (1/2)AC = (1/2) * 2√3a = √3a
Trong tam giác vuông C'OH, ta có: tan(C'OH) = C'H / OH tan(60°) = C'H / (OC/2) (vì H là trung điểm OB) √3 = C'H / (√3a / 2) C'H = (3a) / 2 Vậy chiều cao của khối hộp là C'C = C'H = (3a) / 2
Thể tích khối hộp V = diện tích đáy * chiều cao V = (a√6)² * (3a/2) = 6a² * (3a/2) = 9a³ Kết luận: Thể tích của khối hộp chữ nhật đã cho là 9a³.