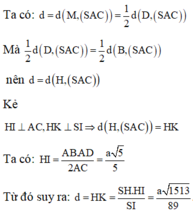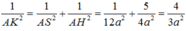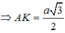Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)
Diện tích tam giác ABD: \({S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích khối hộp là \(V = AA'.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)
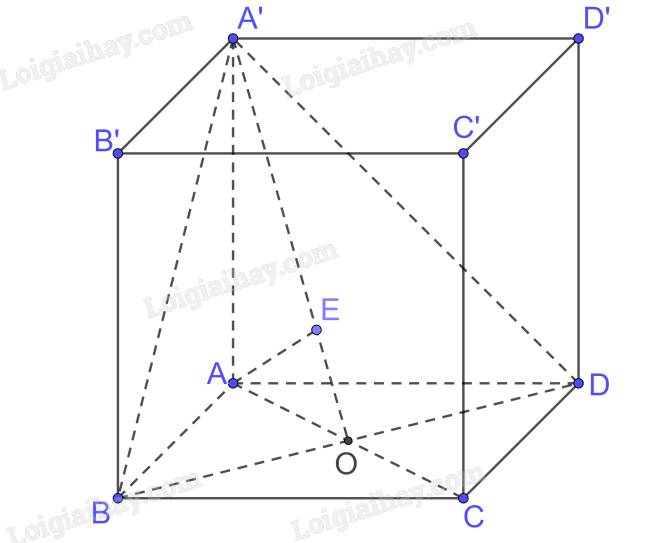
b) Gọi \(AC \cap BD = \left\{ O \right\}\)
Ta có \(AA' \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A'AO} \right);BD \subset \left( {A'BD} \right) \Rightarrow \left( {A'AO} \right) \bot \left( {A'BD} \right)\)
\(\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\)
Trong (A’AO) kẻ \(AE \bot A'O\)
\( \Rightarrow AE \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AE\)
Xét tam giác ABD có AB = AD và \(\widehat {BAD} = {60^0}\) nên tam giác ABD đều
\( \Rightarrow OA = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác AOA’ vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{{A'}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}\)
Vậy \(d\left( {A,\left( {A'BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\)

Chọn D.
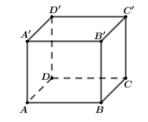
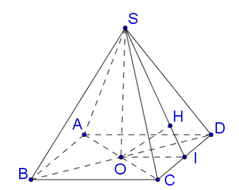
Xét hình chóp AA'BD có AA' = AB = AD và đôi một vuông góc với nhau nên
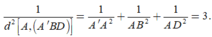
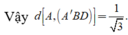

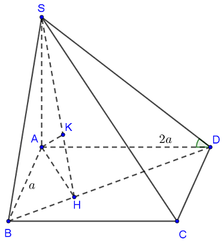
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
Gọi O là tâm đáy \(\Rightarrow AO=CO\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)\)
Kẻ AH vuông góc BD, kẻ AK vuông góc SH
\(\Rightarrow AK\perp\left(SBD\right)\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{1}{a^2}+\dfrac{1}{4a^2}=\dfrac{5}{4a^2}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\)
\(\Rightarrow AK=\dfrac{2a}{3}\Rightarrow d\left(C;\left(SBD\right)\right)=\dfrac{2a}{3}\)

Đáp án B.
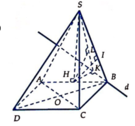
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
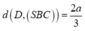
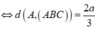
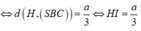
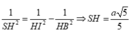
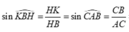
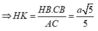
![]()
![]()
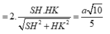

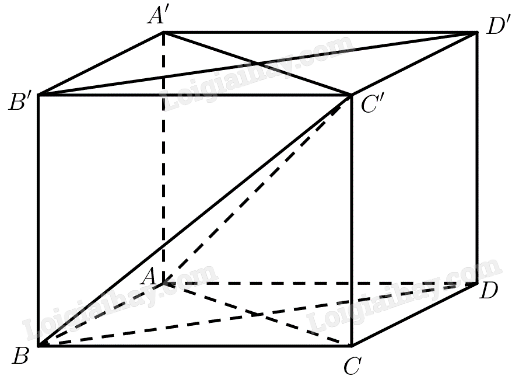
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).

Đáp án C
Gọi O = AC ∩ BD Kẻ OK ⊥ SC Do BD ⊥ (SAC) =>BD ⊥ OK
Do đó d(BC;SC) =OK= a 3 2
∆ S A C đ ồ n g d ạ n g ∆ O K C ( g - g )
⇒ S A O K = S C O C ⇔ x a 3 2 = x 2 + 12 a 2 a 3
⇒ x 2 = 6 a 2 ⇒ x = a 6 ⇔ S A = a 6
Khi đó: Kẻ AH ⊥ SD => AH ⊥ (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
∆ S A D vuông tại A có 1 A H 2 = 1 A S 2 + 1 A D 2 ⇒ A H = a 2