Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có ![]()
Xét hàm ![]()
Tập xác định D = (0; 10).
![]()
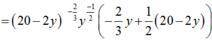
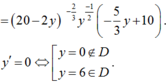
Nhận xét: ![]() nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức ![]()
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy ![]()

Lời giải:
Theo như đề thì hàm lợi nhuận (y) và sản lượng (x) sẽ có dạng này:
Hàm lợi nhuận có dạng pt như sau:
$y=ax^2+bx+c$
Sản lượng bằng $0$ thì lợi nhuận đương nhiên bằng $0$
$\Rightarrow c=0$
ĐTHS đổi dấu tại $x=10$, tức là $x=10$ là điểm cực trị
$\Rightarrow \frac{b}{-2a}=10\Leftrightarrow b=-20a$
$y=ax^2-20ax$. Thay $x=5; y=170$ thì $a=-\frac{34}{15}$
Vậy hàm lợi nhuận là: $y=\frac{-34}{15}x^2+\frac{136}{3}x$
Tại $x=12$ thì $y=217,6$
Hàm lợi nhuận giảm với tốc độ là \(|y'(12).\frac{12}{217,6}|=0,5\) (%)
Vậy tại mức sản phẩm 12, khi mức sản phẩm tăng 1% thì lợi nhuận giảm 0,5 %.

Giá của x sản phẩn là:
x ( 120 -x ) = - x2 +120x
Lợi nhuận còn lại:
\(-x^2+120x-C\left(x\right)=-x^2+120x-x^2-5x-300=-2x^2+115x-300\)

TOÁN LỚP 12 ?????
4346000X18:100=782280(ĐỒNG)
=>GIÁ BÁN CÁI TI VI LÀ
4346000+782280=5128280(ĐỒNG)
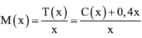
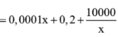
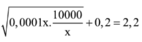
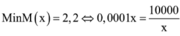
Chúng ta cần tìm mức giá bán p tối ưu để tối đa hóa lợi nhuận P(x) . Các thông tin được cung cấp như sau: 1. Số lượng ti vi bán ra ban đầu: x_0 = 1000 . 2. Giá bán ban đầu: p_0 = 14 \, \text{triệu đồng} . 3. Nếu giảm giá 500 \, \text{nghìn đồng}, số lượng bán tăng thêm 100 chiếc mỗi tuần. 4. Hàm chi phí: C(x) = 12,000 + 3x (triệu đồng). 5. Hàm doanh thu: R(x) = p \cdot x , với p là giá bán một chiếc ti vi và x là số lượng bán ra. Phân tích bài toán: 1. Hàm giá bán: Giá bán p phụ thuộc vào số lượng bán ra x . Mỗi khi x tăng thêm 100, giá giảm 0.5 triệu đồng: p(x) = 14 - 0.5 \cdot \frac{x - 1000}{100} = 14 - 0.005(x - 1000). 2. Hàm lợi nhuận P(x) : P(x) = R(x) - C(x). Với R(x) = p(x) \cdot x , ta có: R(x) = \left(14 - 0.005(x - 1000)\right) \cdot x. Sau đó: P(x) = R(x) - (12,000 + 3x). Tìm giá trị x tối ưu bằng cách tối đa hóa P(x)
Mình lười tính quá nên gợi í thôi ạ