Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Người A nên hỏi người B là “anh đi từ hướng nào đến”.
Vì khi người A hỏi người B như vậy, có nghĩa là nếu người B là người ở làng nói dối sẽ chỉ về hướng làng nói thật,
Còn nếu người B là người ở làng nói thật cũng sẽ chỉ về làng nói thật.
Vì vậy ta biết được hướng nào là hướng về ngôi làng nói thật và hướng nào dẫn đến ngôi làng nói dối.
Bài nay hay thật đấy![]()

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)

1. con người
2. bác tài bỏ lại xe đó và đi qua cầu
3. vì chúng bò theo đường thẳng nằm ngang
4.tôi sẽ bị treo cổ
5. đập con ma xanh trước, con ma đỏ thấy thế sợ quá mặt mày chuyển sang màu xanh, đập thêm phát nữa là chết cả 2 con.
6. con cua xanh vì cua đỏ đã được luộc chín rồi.

Tham khảo:
a) Gọi x là số thùng thuốc trừ sâu loại A, y là số thùng thuốc trừ sâu loại B mà nhà máy sản xuất mỗi ngày. Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- sản lượng \(C{O_2}\) tối đa là 75 kg nên \(0,25x + 0,5y \le 75\)
- sản lượng \(S{O_2}\) tối đa là 90 kg nên \(0,6x + 0,2y \le 90\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}0,25x + 0,5y \le 75\\0,6x + 0,2y \le 90\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
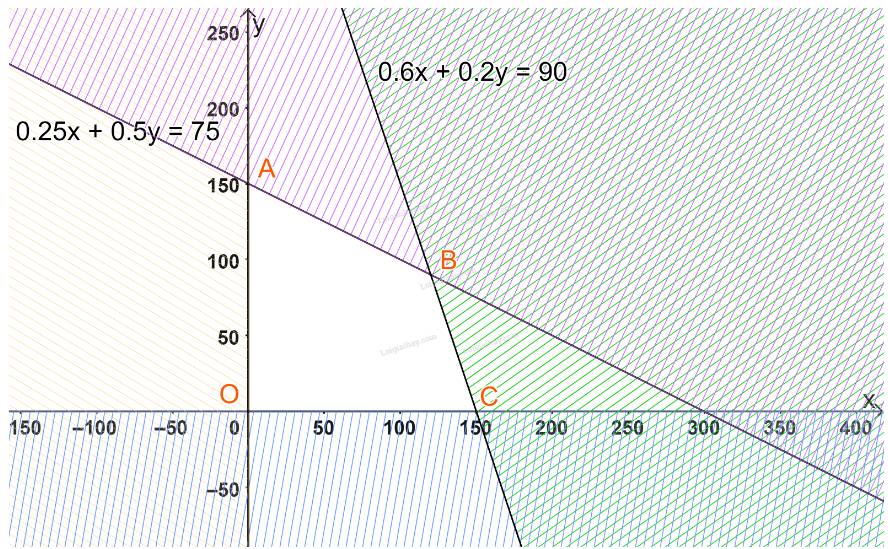
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
b) Nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày tức là \(x = 100,y = 80.\)
Vì \(\left\{ \begin{array}{l}0,25.100 + 0,5.80 = 65 \le 75\\0,6.100 + 0,2.80 = 76 \le 90\\100 \ge 0\\80 \ge 0\end{array} \right.\) nên cặp số (100; 80) là một nghiệm của hệ bất phương trình a).
Do đó việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày là phù hợp với quy định.
c) Vì \(0,25.60 + 0,5.160 = 95 > 75\)nên việc sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày vượt quá sản lượng \(C{O_2}\) tối đa.
Vậy việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày là không phù hợp với quy định.

Việc thực hiện bữa trưa gồm một món chính, một món phụ và một loại đồ uống gồm 3 công đoạn
Công đoạn 1: Chọn 1 món chính trong 5 món, có 5 cách chọn
Công đoạn 2: Chọn 1 món phụ trong 3 món, có 3 cách chọn
Công đoạn 3: Chọn 1 loại đồ uống trong 4 loại, có 4 cách chọn
Áp dụng quy tắc nhân, ta có số cách chọn một bữa trưa đầy đủ là
\(5.3.4 = 60\)
Vậy có 60 cách chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống.

Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
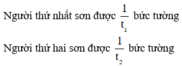
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có: 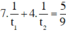
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình 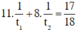
Ta có hệ phương trình 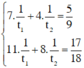
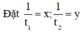 , khi đó hệ phương trình trở thành
, khi đó hệ phương trình trở thành 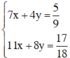
Giải hệ phương trình trên ta được 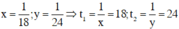
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.


Đây là một bài toán nổi tiếng có tên là Bài toán của Einstein (hay còn gọi là "Bài toán ngôi nhà màu sắc"), được cho là do Albert Einstein sáng tạo ra. Mục tiêu của bài toán là xác định ai là người nuôi cá dựa trên một số thông tin được cho. Để giải quyết bài toán, ta sẽ sử dụng phương pháp suy luận và kết hợp các giả thiết đã cho. Các thông tin đã biết: Có 5 ngôi nhà, mỗi ngôi nhà có một màu sắc khác nhau. Chủ nhân của mỗi ngôi nhà mang quốc tịch khác nhau. Mỗi người thích một loại nước uống khác nhau. Mỗi người hút một loại thuốc lá khác nhau. Mỗi người nuôi một loại vật nuôi khác nhau. Câu hỏi: Ai là người nuôi cá? Để giải quyết bài toán, ta có thể sắp xếp các thông tin vào một bảng và từ đó sử dụng suy luận để đi đến kết luận. Các yếu tố: Màu sắc của ngôi nhà Quốc tịch của chủ nhân Loại nước uống yêu thích Hãng thuốc lá hút Loại vật nuôi Các giả thiết (dữ liệu bài toán): Người Anh sống trong ngôi nhà màu đỏ. Người Thụy Điển nuôi chó. Người Đan Mạch uống trà. Ngôi nhà màu xanh lá cây nằm bên cạnh ngôi nhà màu trắng. Chủ nhân của ngôi nhà màu xanh lá cây uống cà phê. Người Nhật Bản hút thuốc lá "Marlboro". Người người Đức hút thuốc lá "Prince". Người sống trong ngôi nhà màu vàng hút thuốc lá "Dunhill". Người sống trong ngôi nhà màu trắng nuôi cá. Người sống trong ngôi nhà màu xanh lá cây nuôi chim. Phương pháp giải: Bằng cách kết hợp các giả thiết, ta có thể xây dựng một bảng như sau: Nhà Màu sắc Quốc tịch Nước uống Thuốc lá Vật nuôi 1 Màu vàng Đan Mạch Trà Dunhill Mèo 2 Màu xanh lá Đức Cà phê Prince Chim 3 Màu đỏ Anh Sữa Marlboro Ngựa 4 Màu trắng Thụy Điển Nước trái cây Blue Master Cá 5 Màu xanh Nhật Bản Bia Dunhill Chó Kết luận: Dựa trên bảng trên, ta có thể thấy rằng người sống trong ngôi nhà màu trắng là người Thụy Điển và họ nuôi cá.
Thanks Hoàng nha