Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(T\left( x \right)\) xác định trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số \(T\left( x \right)\) xác định trên từng khoảng \(\left( {0;0,7} \right),\left( {0,7;20} \right)\) và \(\left( {20; + \infty } \right)\) nên hàm số liên tục trên các khoảng đó.
Ta có: \(T\left( {0,7} \right) = 10000\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0,{7^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ + }} \left( {10000 + \left( {x - 0,7} \right).14000} \right) = 10000 + \left( {0,7 - 0,7} \right).14000 = 10000\\\mathop {\lim }\limits_{x \to 0,{7^ - }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ - }} 10000 = 10000\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 0,{7^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ - }} T\left( x \right) = 10000\) nên \(\mathop {\lim }\limits_{x \to 0,7} T\left( x \right) = 10000 = T\left( {0,7} \right)\).
Vậy hàm số \(T\left( x \right)\) liên tục tại điểm \({x_0} = 0,7\).
Ta có: \(T\left( {20} \right) = 10000 + \left( {20 - 0,7} \right).14000 = 280200\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {{20}^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ + }} \left( {280200 + \left( {x - 20} \right).12000} \right) = 280200 + \left( {20 - 20} \right).12000 = 280200\\\mathop {\lim }\limits_{x \to {{20}^ - }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ - }} \left( {10000 + \left( {x - 0,7} \right).14000} \right) = 10000 + \left( {20 - 0,7} \right).14000 = 280200\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to {{20}^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ - }} T\left( x \right) = 280200\) nên \(\mathop {\lim }\limits_{x \to 20} T\left( x \right) = 280200 = T\left( {20} \right)\).
Vậy hàm số \(T\left( x \right)\) liên tục tại điểm \({x_0} = 20\).
Vậy hàm số \(T\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\).

Để tính giá thành làm cầu thang, ta cần tính diện tích của từng bậc thang và sau đó cộng lại.
Diện tích của một bậc thang có thể tính bằng công thức: Diện tích = Chiều dài x Chiều rộng.
Ta có thể tính diện tích của từng bậc thang như sau:
Bậc đầu tiên: Diện tích = 189cm x 35cm = 6615cm² Bậc thứ hai: Diện tích = (189cm - 7cm) x 35cm = 6230cm² Bậc thứ ba: Diện tích = (189cm - 2*7cm) x 35cm = 5845cm² ... Bậc cuối cùng: Diện tích = 63cm x 35cm = 2205cm²
Sau đó, ta cộng lại diện tích của từng bậc thang để tính tổng diện tích cầu thang:
Tổng diện tích = 6615cm² + 6230cm² + 5845cm² + ... + 2205cm²
Để tính giá thành của cầu thang, ta nhân tổng diện tích cầu thang với giá thành một mét vuông:
Giá thành = Tổng diện tích x 1250000 đồng/m²
Vì không có thông tin cụ thể về số bậc thang trong câu hỏi, nên không thể tính được tổng diện tích và giá thành chính xác. Tuy nhiên, để xác định giá thành gần với số nào dưới đây, ta có thể ước lượng giá thành bằng cách lấy diện tích trung bình của các bậc thang và nhân với số bậc thang.
Giả sử số bậc thang là n, ta có:
Diện tích trung bình = (6615cm² + 6230cm² + 5845cm² + ... + 2205cm²) / n
Giá thành ước lượng = Diện tích trung bình x 1250000 đồng/m²

Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).

a, Nếu tỉ lệ lạm phát 8% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại
\(A=100\cdot\left(1-\dfrac{8}{100}\right)^2=84,64\) (triệu đồng)
b, Nếu sức mua của 100 triệu đồng sau hai năm chỉ còn là 90 triệu đồng thì
\(90=100\cdot\left(1-\dfrac{r}{100}\right)^2\Leftrightarrow\left(1-\dfrac{r}{100}\right)^2=0,9\Leftrightarrow r\approx5,13\)
Vậy nếu sức mua của 100 triệu đồng sau hai năm chỉ còn là 90 triệu đồng thì tỉ lệ lạm phát trung bình của hai năm đó là khoảng 5,13%.
c) Nếu tỉ lệ lạm phát là 5% một năm và sức mua của số tiền ban đầu chỉ còn lại một nửa ta có
\(\dfrac{P}{2}=P\cdot\left(1-\dfrac{5}{100}\right)^n\Leftrightarrow\left(\dfrac{19}{20}\right)^n=\dfrac{1}{2}\\
\Leftrightarrow n=log_{\dfrac{19}{20}}\left(\dfrac{1}{2}\right)\approx13,51\)
Vậy nếu tỉ lệ lạm phát là 5% một năm thì sau 14 năm sức mua của số tiền ban đầu chỉ còn lại một nửa.

Đáp án A
Số cách sắp xếp 50 câu cho một đề thi là 50!
Số cách chọn 20 câu nhận biết để xếp chúng vào đầu tiên là: 20!
Số cách chọn 10 câu thông hiểu để xếp chúng vào vị trí thứ hai là 10!
Số cách chọn 15 câu vận dụng để xếp chúng vào vị trí thứ ba là 15!
Số cách chọn 5 câu vận dụng cao xếp chúng vào vị trí cuối cùng là 5!
=> Xác suất cần tìm được tính bằng: P = 20 ! . 10 ! . 15 ! . 5 ! 50 ! = 4,56.10-26
=> Chọn phương án A.

a) Công thức tính giá trị của ô tô:
- Sau 1 năm: \(800 - 800.4\% = 768\) (triệu đồng)
- Sau 2 năm: \(768 - 768.4\% = 737,28\) (triệu đồng)
b) Công thức tính giá trị của ô tô sau n năm sử dụng: \({S_n} = 800{\left( {1 - 0,04} \right)^n}\)
c) Sau 10 năm, giá trị của ô tô ước tính còn: \({S_{10}} = 800{\left( {1 - 0,04} \right)^{10}} \approx 531,87\) (triệu đồng)


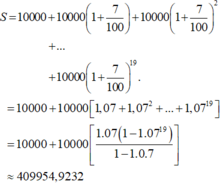
cứu em với mn ạ!
Vì cứ 10 km là 1 bậc nên từ khi xuất phát đến khi đi hết 114 km có số bậc là:
[\(\dfrac{114}{10}\)] + 1 = 12 (bậc) với \(\left[\dfrac{114}{10}\right]\) là giá trị nguyên của 114 chia 10
Giá tiền mỗi ki-lô-mét của mỗi bậc sau so với bậc trước bằng:
100% - 5% = 95%
95% = 0,95
Vì giá tiền mỗi ki-lô-mét bậc sau bằng 0,95 lần giá tiền bậc trước nên nếu giá tiền mỗi ki-lô-mét bậc 1 là \(x\) thì giá tiền của mỗi ki-lô-mét của các bậc tiếp theo lần lượt là: 0,95\(x\); 0,952\(x\);...0,95n\(x^{ }\)
Tổng số tiền cần thanh toán khi đi hết n bậc là:
A = 10x(\(x\) + 0,95\(x\) + 0,952\(x\) ....+ 0,95\(^{n-1}\)\(x\)) (1)
Cứ 10 km là một bậc nên số ki-lô-mét đi ở bậc thứ 12 là:
114 - 10 x (12 - 1) = 4 (km)
Số tiền cần trả cho 4 km ở bậc thứ 12 là:
10000 x 4 x \(0,95^{12-1}\) ≈ 22752 (đồng)
Áp dụng công thức (1) trên ta có số tiền Cần trả cho hãng xe khi đi hết 11 bậc ứng với 110km là:
10x10000x(1+0,95+0,952+...+0,95\(^{11-1}\)) ≈ 862400 (đồng)
Số tiền cần trả cho 114 km là: 22752 + 862400 = 885152 (đồng)
Số tiền An cần trả cho 50 km khi đi một mình là:
10 x 10000 x (1+ 0,95 + 0,952 + ...+ 0,955-1) ≈ 452438 (đồng)
Số tiền mình An cần trả cho cho cả quãng đường 114 km là:
452438 + (885152 - 452438) x 20% = 538980,8 (đồng)
538980,8 đồng làm tròn đến hàng nghìn là: 539 000 đồng
Vậy số tiền An cần thanh toán khi đi hết quãng đường 114 km là
539 000 đồng.