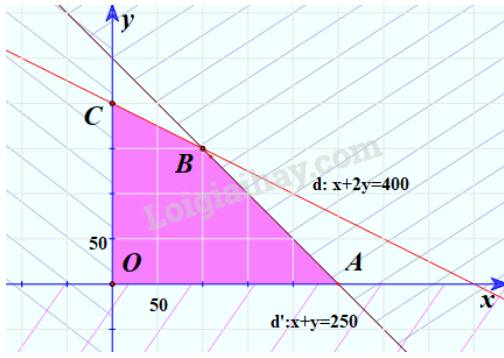
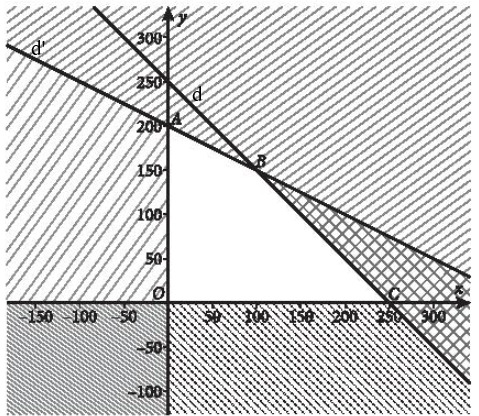
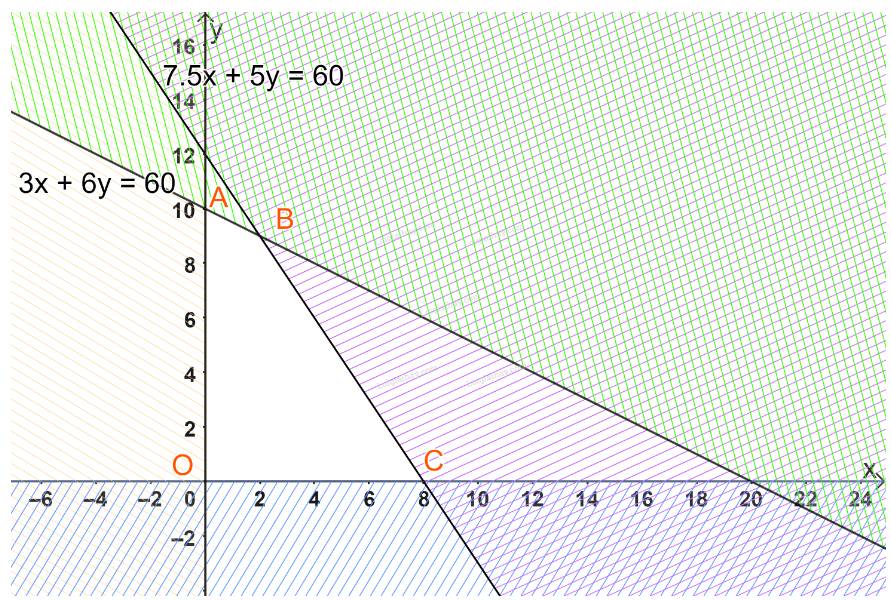
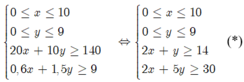- Sản xuất ít nhất 12 viên kim cương to: 5x + 2y ≥ 12
- Sản xuất ít nhất 9 viên kim cương nhỏ: 3x + 3y ≥ 9 hay x + y ≥ 3
- Sử dụng tối đa 4 tấn Cacbon mỗi loại: 0 ≤ x ≤ 4 và 0 ≤ y ≤ 4
- Tổng tiền mua Cacbon không vượt quá 500 triệu đồng: Giả sử giá mỗi tấn Cacbon loại 1 là a triệu đồng và giá mỗi tấn Cacbon loại 2 là b triệu đồng, ta có ràng buộc: ax + by ≤ 500. Tuy nhiên, đề bài không cung cấp giá của mỗi loại Cacbon, nên ta tạm bỏ qua ràng buộc này. Chúng ta sẽ giải bài toán với các ràng buộc còn lại và xem xét lại nếu có thêm thông tin