Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giá của x sản phẩn là:
x ( 120 -x ) = - x2 +120x
Lợi nhuận còn lại:
\(-x^2+120x-C\left(x\right)=-x^2+120x-x^2-5x-300=-2x^2+115x-300\)
Chọn C.
Gọi 
là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là nghìn đồng.
Chi phí vận hành 50x nghìn đồng.
Số bản in trong một giờ là 3600x => thời gian để in xong 50000 tờ quảng cáo là 
Vậy tổng chi phí là 
nghìn đồng
Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.
Thay các giá trị x = {1;2;3;4;5;6;7;8} ta thấy giá trị nhỏ nhất là 
Đáp án C
Cách giải:
Nhận xét: Để thu được nhiều lãi nhất thì tổng chi phí bảo trì, chi phí in ấn là ít nhất.
Gọi số máy in cần sử dụng là n (máy), n ∈ N; n ∈ (0;8)
Số giờ cần để in hết 50 000 bản in là: 
Chi phí để n máy hoạt động trong 25 2 n giờ là:
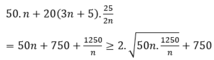
=> n = 5
Vậy, nếu in 50 000 bản in khổ A4 thì phải sử dụng 5 máy sẽ thu được lãi nhiều nhất.
Gọi số tiền còn lại phải trả sau i tháng là Pi ; A=300 (triệu) là số tiền đã vay ; d=5,5 (triệu) là số tiền trả cố định tháng ; r=0,5% là lãi trên tháng
Ta luôn có, tại thời điểm tháng thứ i, số tiền còn lại phải trả là Pi bằng số tiền còn lại phải trả của tháng trước đó trừ đi tiền lãi ( Pi-1*r ) và trừ thêm tiền trả cố định hàng tháng (d) ; viết gọn lại là \(P_i=P_{i-1}-P_{i-1}\cdot r-d=P_{i-1}\left(1-r\right)-d\)
Áp dụng côn thức trên ta có:
Ngay tại thời điểm vay xong thì \(P_0=A\)
qua tháng thứ nhất : \(P_1=P_0-P_0r-d=A\left(1-r\right)-d\)
qua tháng thứ hai : \(P_2=P_1\left(1-r\right)-d=A\left(1-r\right)^2-d\cdot\left[\left(1-r\right)+1\right]\)
.....
qua tháng thứ k : \(P_k=P_{k-1}\left(1-r\right)-d=A\left(1-r\right)^k-d\cdot\left[\left(1-r\right)^{k-1}+\left(1-r\right)^{k-2}+...+\left(1-r\right)+1\right]\\ =A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}\)
Xét thời điểm trả hết nợ, tức là Pk=0
\(\Leftrightarrow A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}=0\\ \Leftrightarrow300\left(1-0,5\%\right)^k=5,5\cdot\frac{\left(1-0,5\%\right)^k-1}{\left(1-0,5\%\right)-1}\\ \Leftrightarrow\left(1-0,5\%\right)^k=\frac{11}{14}\Leftrightarrow k\approx48,1117\)
Bạn nhớ luôn công thức tren để giải bài tập liên quan nhé
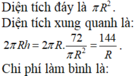
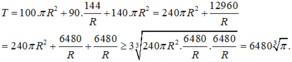
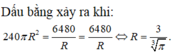
T
Gọi \(x\) (nghìn đồng) là số tiền tăng thêm \(\left(x>0\right)\)
Số tiền mỗi đôi giày là \(65+x\) (nghìn đồng)
Số đôi giày bán được là \(5000-100x\) (đôi) \(\left(x< 50\right)\)
Chi phí cho \(\left(5000-100x\right)\) đôi giày là \(\left(5000-100x\right).50\) (nghìn đồng)
\(\Rightarrow\) Doanh thu \(R\left(x\right)=\left(5000-100x\right)\left(65+x\right)\) (nghìn đồng)
\(\Rightarrow\) Lợi nhuận \(P\left(x\right)=R\left(x\right)-E\left(x\right)=\left(5000-100x\right)\left(x+65-50\right)\) (nghìn đồng)
\(P\left(x\right)=\left(5000-100x\right)\left(x+15\right)\)
\(P\left(x\right)=100\left(50-x\right)\left(x+15\right)\)
\(P\left(x\right)\le100.\left(\dfrac{50-x+x+15}{2}\right)^2=105625\) (nghìn đồng)
Dấu "=" xảy ra \(\Leftrightarrow50-x=x+15\Leftrightarrow x=17,5\) (nhận)
Vậy để mỗi tháng đạt lợi nhuận lớn nhất thì cần bán mỗi đôi giày giá \(65+17,5=82,5\) (nghìn đồng)