Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Kẻ đường kính chứa 1 trong 3 điểm A,B,C bất kỳ của (O)
Tam giác ABC chứa tâm O <=>
(*) Có nhiều nhất 2 điểm nằm
trên nửa đường tròn (O) có đường kính như trên , không nhận
cạnh nào là đường kính
(*) ABC là tam giác vuông
Nhận thấy khi tam giác ABC nội tiếp (O) thì A,B,C có 3 trường hợp:
TH1 : 3 điểm cùng nằm trên nửa (O ; DE/2) , không có cạnh nào là đường kính
TH2 : 2 điểm nằm trên nửa (O ; DE/2) ; 1 điểm trên nửa (O) còn lại
TH3 : Tam giác vuông
Biến cố A : " Tam giác ABC chứa tâm O"
=> P(A) = \(\dfrac{2}{3}\)

Vì O là tâm của hình bình hành ABCD
nên O là trung điểm chung của AC và BD
=>\(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0};\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\dfrac{1}{4}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right)\)
\(=\dfrac{1}{4}\left(\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\right)\)
\(=\dfrac{1}{4}\left(4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}+\overrightarrow{OD}\right)\)
\(=\dfrac{1}{4}\cdot4\overrightarrow{MO}=\overrightarrow{MO}\)

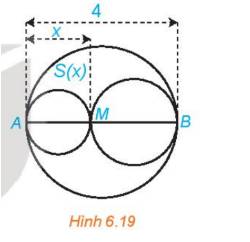
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
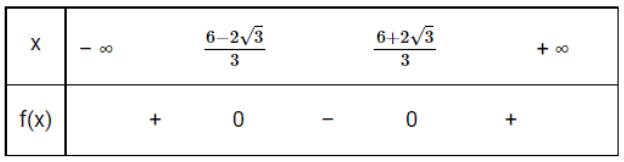
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)

I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)

Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(7;-4\right)\\\overrightarrow{DC}=\left(3-x;7-y\right)\end{matrix}\right.\)
ABCD là hbh khi: \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}3-x=7\\7-y=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-4\\y=11\end{matrix}\right.\)
\(\Rightarrow D\left(-4;11\right)\)

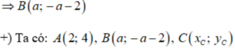

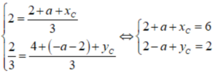
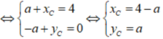
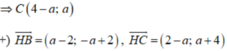
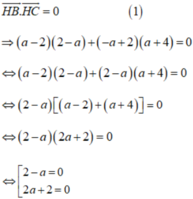
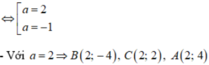
No cứ bảo phải là khách VIP
Trước hết, ta xét phiên bản 2D của bài toán này như sau:
Bài toán: Lấy 3 điểm A, B, C bất kì nằm trên đường tròn (O). Tính xác suất để O nằm trong tam giác ABC.
Giải: Cố định điểm A. Hai đường kính bất kì khác nhau của (O) cắt đường tròn tại 4 vị trí. Khi đó sẽ có 2 cách chọn điểm B và C trong 4 giao điểm, tức là sẽ có \(2^2=4\) cách khác nhau để "đặt" 2 điểm B, C.
Trong 4 vị trí thì chỉ có 1 vị trí thỏa mãn tam giác ABC chứa O. Vì 3 điểm A, B, C đều xuất hiện ở các vị trí khác nhau trên đường tròn vớ khả năng như nhau nên xác suất để tam giác ABC chứa O là \(\dfrac{1}{4}\).
Trở lại bài toán, ta cũng lập luận tương tự: Cố định một điểm. Khi đó 3 đường kính bất kỳ của mặt cầu cắt mặt cầu tại 6 điểm. Khi đó mỗi 1 trong 3 điểm còn lại đều có 2 cách chọn nên có tất cả \(2^3=8\) cách chọn 3 điểm. Trong 8 cách chọn thì chỉ có 1 cách thỏa mãn tứ diện ABCD chứa tâm mặt cầu. Do khả năng xuất hiện của 4 điểm ở tất cả các vị trí trên mặt cầu là như nhau nên xác suất để tâm hình cầu nằm trong tứ diện bằng \(\dfrac{1}{8}\).
Vậy xác suất để tâm mặt cầu nằm trong tứ diện là \(\dfrac{1}{8}\).