Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(x^2+\dfrac{v^2}{w^2}=A^2\)
\(\Rightarrow A^2=0,24^2+\dfrac{2,8^2}{40^2}=\dfrac{1}{16}\\ \Rightarrow A=0,25\left(m\right)=25cm\)

\(\omega=20\left(\dfrac{rad}{s}\right)\)
\(A^2=x^2+\dfrac{v^2}{\omega}\)
\(\Rightarrow A=\sqrt{\left(-4\right)^2+\dfrac{\left(-80\right)^2}{20^2}}=4\sqrt{2}\)
\(cos\varphi=\dfrac{4}{4\sqrt{2}}=\dfrac{1}{\sqrt{2}}\Rightarrow\varphi=\dfrac{\pi}{4}\)
Phương trình dao động:
\(x=4\sqrt{2}cos\left(20t+\dfrac{\pi}{4}\right)\)

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)

Giả sử pt dao động của vật có dạng:
\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)
\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)
Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)
\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)
Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)
b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)
\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)
c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)
\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)

1)
Với phương trình vị trí `x = 3cos(4πt)`, ta có:
`dx/dt = -12πsin(4πt)`
Phương trình vận tốc của vật dao động là:
`v = -12πsin(4πt) (cm)/s`
Với phương trình vận tốc v = -12πsin(4πt), ta có:
`(dv)/dt = -48π^2cos(4πt)`
Phương trình gia tốc của vật dao động là:
`a = -48π^2cos(4πt) (cm)/s^2`

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)

a) Li độ \(x=4cm=\dfrac{A}{2}\):
\(\omega=5rad/s\)
Động năng:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2\left(A^2-x^2\right)=\dfrac{1}{2}\cdot2\cdot5^2\left(0,08^2-0,04^2\right)\approx0,03J\)
Cơ năng: \(W=\dfrac{1}{2}mv^2_{max}=\dfrac{1}{2}\cdot2\cdot5^2\cdot0,08^2=0,16J\)
Thế năng: \(W_t=W-W_đ=0,16-0,03=0,13J\)
b)Để thế năng bằng động năng: \(W_đ=W_t\)
\(\Rightarrow\dfrac{1}{2}m\omega^2\left(A^2-x^2\right)=\dfrac{1}{2}m\omega^2x^2\)
\(\Rightarrow A^2-x^2=x^2\Rightarrow A^2=2x^2\Rightarrow x=\pm\dfrac{A}{\sqrt{2}}\)
a) Động năng của vật được tính bằng công thức:
K = (1/2) * 2 * (5)^2 * (0.04)^2 ≈ 0.008 J
U = (1/2) * 2 * (5)^2 * (0.08)^2 - (1/2) * 2 * (5)^2 * (0.04)^2 ≈ 0.032 J. Vậy động năng của vật là khoảng 0.008 J và thế năng của vật là khoảng 0.032 J.
b) Để tìm li độ mà thế năng bằng động năng, ta giải phương trình U = K: (1/2) * 2 * (5)^2 * A^2 - (1/2) * 2 * (5)^2 * x^2 = (1/2) * 2 * (5)^2 * x^2 (1/2) * 2 * (5)^2 * A^2 = (1/2) * 2 * (5)^2 * x^2 + (1/2) * 2 * (5)^2 * x^2 (1/2) * 2 * (5)^2 * A^2 = 2 * (1/2) * 2 * (5)^2 * x^2 A^2 = 2 * x^2 A = √(2 * x^2) Vậy thế năng bằng động năng khi li độ x = A/√2.
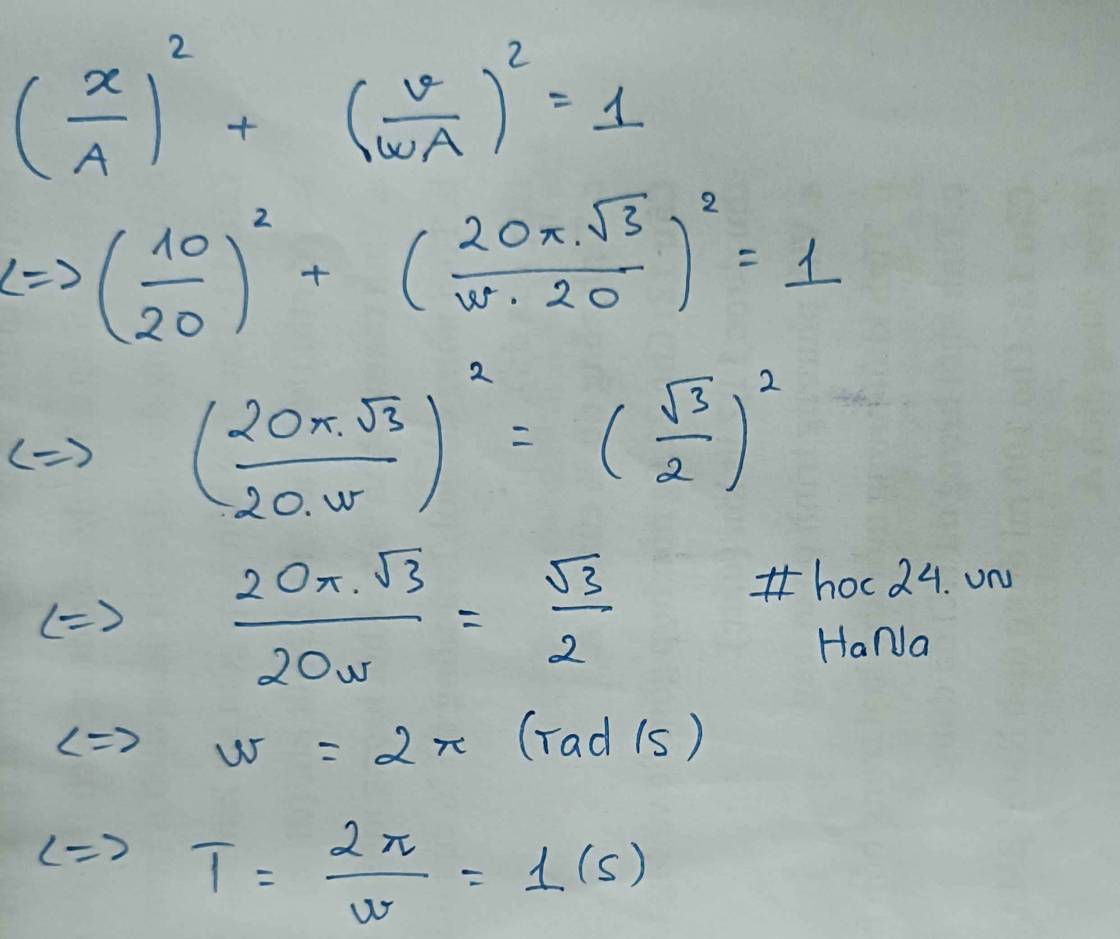
#Hoàng Nam
bn bị down à
hay não không có chất xám
Trl câu hỏi down chưa từng thấy