Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Gọi số tiền ông Sáu gửi ban đầu là x.
Theo đề bài ta có:
Số tiền lãi sau 1 năm ông Sáu nhận được là : 0,06x (đồng)
Số tiền lãi có được 1 năm của ông Sáu là : x + 0,06x = 1,06x (đồng)
Số tiền lãi năm thứ 2 ông Sáu nhận được là : 1,06x. 0,06 = 0,0636x (đồng)
Do vậy, số tiền tổng cộng sau 2 năm ông Sáu nhận được là : 1,06x + 0,0636x = 1,1236x (đồng)
Mặt khác: 1,1236x = 112360000 nên x = 100000000(đồng) hay 100 triệu đồng
Vậy ban đầu ông Sáu đã gửi 100 triệu đồng.
Tổng % lãi suất trong 2 năm là :
6% . 2 = 12%
Số tiền lãi trong 2 năm là :
112360000 . 12% = 13483200
=> Tiền ông Sáu gửi là :
112360000 - 13483200 = 98876800

a) \(A=\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}+\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3}+1\right)^2}}+\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\frac{2-\sqrt{3}}{1+\sqrt{3}+1}+\frac{2+\sqrt{3}}{1-\sqrt{3}+1}\)
\(=\frac{2-\sqrt{3}}{2+\sqrt{3}}+\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\frac{\left(2-\sqrt{3}\right)\left(2-\sqrt{3}\right)+\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\frac{4-4\sqrt{3}+3+4+4\sqrt{3}+3}{4-3}\)
\(=14\)
a) A = \(\frac{2-\sqrt{3}}{1+\sqrt{4+2\sqrt{3}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{4-2\sqrt{3}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+2\sqrt{3.1+1}}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3-2\sqrt{3.1+1}}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{\left(\sqrt{3+1}\right)^2}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{\left(\sqrt{3-1}\right)^2}}\) = \(\frac{2-\sqrt{3}}{1+\sqrt{3+1}}\) + \(\frac{2+\sqrt{3}}{1-\sqrt{3+1}}\) = \(\frac{2-\sqrt{3}}{2+\sqrt{3}}\) + \(\frac{2+\sqrt{3}}{2-\sqrt{3}}\) = \(\frac{\left(4-4\sqrt{3+3}\right)+\left(4+4\sqrt{3+3}\right)}{4-3}\) = \(\frac{14}{1}\) = 1

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

Gọi x,y,z là số đồng tiền các loại mệnh giá 2000 đồng, 1000 đồng và 500 đồng. (\(\left(x,y,z\in N^{\circledast}\right)\).
Theo giả thiết ta có: \(x+y+z=1450\) (đồng).
Do tổng số tiền cần đổi là 1 500 000 đồng nên:
\(2000x+1000y+500z=1500000\)
Do số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng nên:\(y=2\left(z-x\right)\)
Vậy ta có hệ:
\(\left\{{}\begin{matrix}x+y+z=1450\\2000x+1000y+500z=1500000\\y=2\left(z-x\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=350\\y=500\\z=600\end{matrix}\right.\)
vậy số tiền loại 2000 đồng là 350 tờ; số tiền loại 1000 đồng là 500 tờ; số tiền loại 600 đồng là 600 tờ.

Số tiền mua x chiếc điều hòa hai chiều là 20x (triệu đồng)
Số tiền mua y chiếc điều hòa một chiều là 10y (triệu đồng).
Số tiền khi mua x chiếc điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
a) Nhu cầu thị trường không quá 100 máy cả 2 loại có nghĩa là tổng số điều hòa nhập vào cũng không quá 100 máy: \(x + y \le 100\)
b)
1,2 tỉ đồng =1200 (triệu đồng)
Số vốn mua x điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên ta có: \(20x + 10y \le 1200\)
\( \Leftrightarrow 2x + y \le 120\)
c)
Số tiền lãi khi bán x chiếc điều hòa hai chiều là 3,5x (triệu đồng)
Số tiền lãi khi bán y chiếc điều hòa một chiều là 2y (triệu đồng)
Tổng số tiền lãi là 3,5x+2y (triệu đồng)

Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình:
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được:
3 x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7 x + 4 y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được:
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

Sau khi mua thì Cường còn lại \(\frac{3}{5}=\frac{15}{25}\) số tiền, Huy còn lại \(\frac{5}{7}=\frac{15}{21}\) số tiền.
Ta thấy thấy tiền của Cường có 25 phần thì tiền của Huy có 21 phần.
Giá trị 1 phần là:
219000:(15+15)=7300 (đồng)
Tiền của Cường có được là:
7300x25=182500(đồng)
Tiền của Huy có được là:
7300x21=153300 (đồng)
Đáp số:153300 đồng

Gọi số tiền mẹ cho anh là a;số tiền mẹ cho em là b
Ta có a-2/3a=b-3/4b
=>1/3a=1/4b
=>a=1/4b:1/3
=>a=3/4b
Mà a+b=105000
Hay 3/4b+b=105000
=>7/4b=105000
=>b=105000:7/4
=>b=60000
=>a=105000-60000
=>a=45000
Vậy mẹ đã cho cho anh 45000 đồng;cho em 60000 đồng

Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
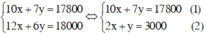
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.
Dì Ly mang 100000 đồng đi mua cam. Dì mua 8 quả cam, trung bình mỗi quả nặng 0,25 kg. Biết mỗi kg cam là 35000 đồng. Tính số tiền dì Ly còn lại sau khi mua cam\(\left[{}\begin{matrix}&&&&\\&&&&\end{matrix}\right.\begin{matrix}\\\\\\\end{matrix}\right.\)

Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
\(10x+7y=17800\)
\(12x+6y=18000\)
<=> Hệ phương trình \(10x+7y=17800\)
\(2x+y=3000\)
<=> Hệ phương trình 2x + y = 3000
2y = 28000
<=> x= 800 và y = 1400.
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đông
Vân:10 quả quýt,7 quả cam=17 800 đồng
Lan:12 quả quýt,6 quả cam=18 000 đồng
Nếu cả số quýt và cam của vân mua gấp lên 2 lần thì đc
20 quýt+14 cam=35 600 đồng
-12 quýt+6 cam=18 000đông
=8 quýt+8 cam=17 600 đồng
giá tiền 1 quả quýt là: 17 600 -8=17 592 đồng
giá tiền1 quả cam là: 17 6 00- 17 592 =8
AI TRẢ LỜI TRƯỚC CHO 1 TICK
Đáp án: 1023 đôla.
Sau khi bước ra khỏi cửa hàng thứ 10, Stacy hết sạch tiền. Vậy theo chu kỳ như ở đề bài, trước khi bước vào cửa hàng thứ 10, Stacy có 1024 đôla.
Vì trúng thưởng, số tiền sẽ tăng lên gấp đôi nên sau khi mua sắm ở cửa hàng thứ 9, Stacy có 1024/2 = 512 đôla. Ta có 512 = 1024 - 29.
Trước khi mua sắm ở cửa hàng thứ 9, Stacy có 512 + 1024 = 1536 đôla.
Suy ra, sau lần mua sắm ở cửa hàng thứ 8, Stacy có 1536/2 = 768 đôla. Ta có 768 = 1024 - 28.
Tương tự ở những lần mua sắm trước đó, ta nhận thấy sau khi bước ra khỏi cửa hàng thứ n (0 ≤ n ≤ 10), Stacy có 1024 - 2n đôla.
Ban đầu, tức là Stacy chưa bước vào cửa hàng nào, n lúc này bằng 0.
Suy ra, số tiền tối thiểu ban đầu của Stacy là 1024 - 20 = 1023 đôla.
(Đáp án bài toán trong giải đấu do sinh viên Harvard, MIT tổ chức)