TT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
5 tháng 8 2017
Đáp án C
Đặt m + e x = a ; e x = b a ≥ 0 ; b > 0 ta có:
m + b = a m + a = b ⇔ m + b = a 2 m + a = b 2
⇔ m + b = a 2 b − a = a 2 − b 2 ⇔ m + b = a 2 a − b a + b + 1 = 0 ⇒ m = a 2 − b a = b
( Do a ≥ 0 ; b > 0 )
Khi đó m = b 2 − b b > 0
Do b 2 − b ≥ − 1 4 ∀ b > 0 nên phương trình có nghiệm khi m ≥ − 1 4
Do đó có 10 giá trị nguyên của m ∈ − 1 4 ; 10 thỏa mãn yêu cầu bài toán.
CM
31 tháng 8 2019
Đáp án C.
Phương pháp:
Số nghiệm của phương trình f x = m bằng số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m .
Cách giải:
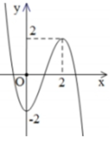
Số nghiệm của phương trình f x = 1 bằng số giao điểm của đồ thị hàm số y = f x và đường thẳng y = 1.
Quan sát đồ thị ta thấy, trên khoảng − ∞ ; 2 đồ thị hàm số y = f x cắt đường thẳng y = 1 tại 2 điểm phân biệt.
Vậy, phương trình f x = 1 có hai nghiệm thực phân biệt nhỏ hơn 2.
LP
3
20 tháng 2 2016
Do 2n+1 là số chính phương lẻ nên 2n+1 chia cho 8 dư 1.
=> n chia hết cho 4. => 3n+1 cũng là một số chính phương lẻ(Do 3n+1 là số chính phương).
=> 3n+1 chia cho 8 dư 1. => 3n chia hết cho 8.
=> n chia hết cho 8( Do (3,8)=1). (1)
-Ta có: 2n+1 và 3n+1 là hai đô chính phương. +Nếu n chia cho 5 dư 4=> 3n+1 chia cho 5 dư 3. => Loại do
số chính phương chia cho 5 chỉ dư 0;1;4. +Nếu n chia cho 5 dư 3=> 2n+1 chia cho 5 dư 2. => Loại.
+Nếu n chia cho 5 dư 2=> 3n+1 chia cho 5 dư 2. => Loại.
+Nếu n chia cho 5 dư 1=> 2n+1 chia cho 5 dư 3. => Loại.
-Từ 4 điều trên và n có tồn tại => n chia hết cho 5. (2)
-Từ (1);(2) => n chia hết cho 8.5= 40.( Do (8,5)=1).
=>n=40 hoặc n=80
Với n=40 =>2n+1 là số chính phương
Với n=80 =>2n+1 không phải là số chính phương
Vậy n=40
26 tháng 2 2016
Số bé nhất mà lớn hơn 2013,5 có hai chữ số ở phần thập phân là 2013,51
Số lớn nhất mà bé hơn 2014,5 có hai chữ số ở phần thập phân là 2014,49
Mỗi số thập phân có hai chữ số ở phần thập phân liên tiếp cách nhau 0,01 đơn vị.
Vậy có tất cả bao nhiêu số thập phân có 2 chữ số ở phần thập phân lớn hơn 2013,5 và nhỏ hơn 2014,5 là :
(2014,49 - 2013,51) : 0,01 + 1 = 99 (số)
LM
27 tháng 2 2016
Số bé nhất mà lớn hơn 2013,5 có hai chữ số ở phần thập phân là 2013,51
Số lớn nhất mà bé hơn 2014,5 có hai chữ số ở phần thập phân là 2014,49
Mỗi số thập phân có hai chữ số ở phần thập phân liên tiếp cách nhau 0,01 đơn vị.
Vậy có tất cả bao nhiêu số thập phân có 2 chữ số ở phần thập phân lớn hơn 2013,5 và nhỏ hơn 2014,5 là :
(2014,49 - 2013,51) : 0,01 + 1 = 99 (số)
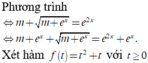
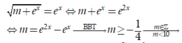
`200 > 196 = 14^2`
Gọi số chính phương đó có dạng: `a^2` với `a >0`
`=> a^2 < 200`
`=> a^2 <= 14^2`
`=> a <= 14`
Số số chính phương thỏa mãn là:
`(14 - 1) : 1 + 1 = 14` (số)
Vậy ...
1; 4; 9; 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196