NV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
Nếu cả 2 đều khác 0 thì em thích tìm theo x hay theo y cũng được, đều đúng
Nhưng thường người ta hay tìm y theo x hơn
NV
2
1 tháng 1 2024
Nếu như theo kiến thức lớp 9 chưa học về đồ thị nào khác ngoài đồ thị bậc nhất (là 1 đường thẳng) thì 2 dạng bài này gần như tương đương nhau. Nhưng khi bạn lên cấp III và học những loại đồ thị đường cong bậc hai (ellipse, parabol, hyperbol, đường tròn,...) thì 2 dạng bài này rõ ràng khác xa nhau nhé. (Vì xác định hàm số thì đó có thể là hàm số kiểu gì cũng được, nhưng viết ptđt thì chỉ có liên quan đến đường thẳng thôi.)
KH
1 tháng 7 2021
Nếu mẫu là \(\left(x+3\right)\left(x-3\right)\) thì điều kiện xác định sẽ là:
\(\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne3\end{matrix}\right.\)
- Lưu ý là cả \(x+3\) và \(x-3\) đều phải khác 0
15 tháng 8 2023
Cái này bạn thay x=0 và y=1 vào rồi ta sẽ có thế này nha:
(m+1)*0+n=1
=>0+n=1
=>n=1
T
27 tháng 2 2019
Mình nghĩ với pt tổng quát: \(ax^2+bx+c=0\) có \(\Delta=b^2-4ac\)
Nếu như vậy thì: \(1.x^2+6x+m\) có \(\Delta=6^2-4m\)chứ?
Riêng mình thì bài này mình dùng delta phẩy cho lẹ:
Lời giải
Để pt \(x^2+6x+m=0\) có 2 nghiệm phân biệt thì:
\(\Delta'=\left(\frac{b}{2}\right)^2-ac=3^2-m>0\)
\(\Leftrightarrow m< 9\)
AH
Akai Haruma
Giáo viên
12 tháng 8 2021
Em không nêu ra yêu cầu và các điều kiện liên quan của đề bài thì làm sao mn giúp em được?
T
12 tháng 7 2019
Em thử nha,sai thì thôi ạ.
2/ ĐK: \(-2\le x\le2\)
PT \(\Leftrightarrow\sqrt{2x+4}-\sqrt{8-4x}=\frac{6x-4}{\sqrt{x^2+4}}\)
Nhân liên hợp zô: với chú ý rằng \(\sqrt{2x+4}+\sqrt{8-4x}>0\) với mọi x thỏa mãn đk
PT \(\Leftrightarrow\frac{6x-4}{\sqrt{2x+4}+\sqrt{8-4x}}-\frac{6x-4}{\sqrt{x^2+4}}=0\)
\(\Leftrightarrow\left(6x-4\right)\left(\frac{1}{\sqrt{2x+4}+\sqrt{8-4x}}-\frac{1}{\sqrt{x^2+4}}\right)=0\)
Tới đây thì em chịu chỗ xử lí cái ngoặc to rồi..
13 tháng 7 2019
1.\(\left(\sqrt{x+3}-\sqrt{x+1}\right)\left(x^2+\sqrt{x^2+4x+3}\right)=2x\)
ĐK \(x\ge-1\)
Nhân liên hợp ta có
\(\left(x+3-x-1\right)\left(x^2+\sqrt{x^2+4x+3}\right)=2x\left(\sqrt{x+3}+\sqrt{x+1}\right)\)
<=>\(x^2+\sqrt{\left(x+1\right)\left(x+3\right)}=x\left(\sqrt{x+3}+\sqrt{x+1}\right)\)
<=> \(\left(x^2-x\sqrt{x+3}\right)+\left(\sqrt{\left(x+1\right)\left(x+3\right)}-x\sqrt{x+1}\right)=0\)
<=> \(\left(x-\sqrt{x+3}\right)\left(x-\sqrt{x+1}\right)=0\)
<=> \(\orbr{\begin{cases}x=\sqrt{x+3}\\x=\sqrt{x+1}\end{cases}}\)
=> \(x\in\left\{\frac{1+\sqrt{13}}{2};\frac{1+\sqrt{5}}{2}\right\}\)
Vậy \(x\in\left\{\frac{1+\sqrt{13}}{2};\frac{1+\sqrt{5}}{2}\right\}\)
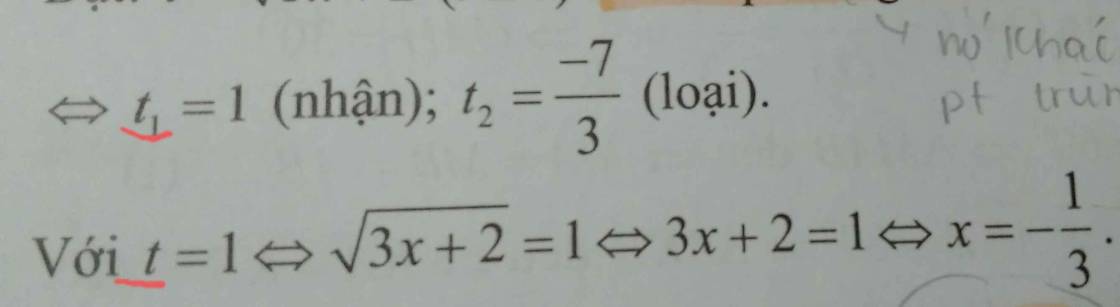
vậy thì phương trình vô nghiệm nha bạn
Phương trình nghiệm đúng với mọi x khác 0