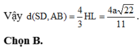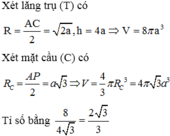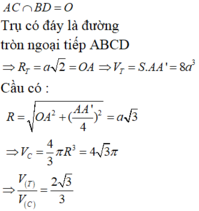Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D A' B' C' D'
\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)

Gọi O là giao điểm của AC và BD \(\Rightarrow A_1O\perp\left(ABCD\right)\)
Gọi E là trung điểm của AD \(\Rightarrow\begin{cases}OE\perp AD\\A_1E\perp AD\end{cases}\)
Suy ra \(\widehat{A_1EO}\) là góc giữa 2 mặt phẳng \(\left(ADD_1A_1\right)\) và \(\left(ABCD\right)\) \(\Rightarrow\widehat{A_1EO}=60^o\)
Suy ra : \(A_1O=OE.\tan\widehat{A_1EO}=\frac{AB}{2}\tan\widehat{A_1EO}=\frac{a\sqrt{3}}{2}\)
Diện tích đáy \(S_{ABCD}=AB.AD=a^2\sqrt{3}\)
Thể tích \(V_{ABCD.A'B'C'D'}=S_{ABCD}.A_1O=\frac{3a^2}{2}\)
Ta có : \(B_1C||A_1D\)\(\Rightarrow B_1C||\left(A_1CD\right)\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=d\left(C,\left(A_1BD\right)\right)=CH\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=CH=\frac{CD.CB}{\sqrt{CD^2+CB^2}}=\frac{a\sqrt{3}}{2}\)

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
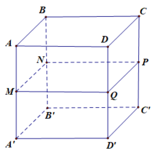
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

Đáp án B
Xét lăng trụ (T) có:
![]()
Xét mặt cầu (C) có: R C = A P 2 = a 3
![]()
Tỉ số bằng 8 4 3 = 2 3 3

Đáp án A
A B C D . A ' B ' C ' D ' nội tiếp khối lăng trụ, ABCD.MNPQ nội tiếp mặt cầu nên
A B C D . A ' B ' C ' D ' là hình hộp chữ nhật
Bán kính đường tròn ngoại tiếp
ABCD là r = 2 a , V T = 4 a . π . 2 a 2 = 8 πa 3
Bán kính mặt cầu ngoại tiếp ABCD.MNPQ là
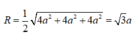
![]()
Vậy V ( T ) V ( C ) = 8 πa 3 4 3 πa 3 = 2 3 3

Phương pháp:
Sử dụng lí thuyết d(a,b) = d(a,(P)) = d(A,(P)), ở đó a,b chéo nhau, (P) chứa b và song song a và A ∈ a để tìm khoảng cách giữa hai đường thẳng SD, AB.
Tính khoảng cách và kết luận.
Cách giải:
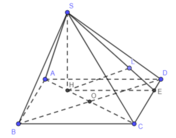
Do AB//CD nên
![]()
![]()
![]()
Kẻ ![]()
![]()
Ta có: SA = 2a, ![]()
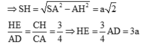
Khi đó ![]()