TV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 4 2022
Bài 2:
a: Để E là số nguyên thì \(3n+5⋮n+7\)
\(\Leftrightarrow3n+21-16⋮n+7\)
\(\Leftrightarrow n+7\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
hay \(n\in\left\{-6;-8;-5;-9;-3;-11;1;-15;9;-23\right\}\)
b: Để F là số nguyên thì \(2n+9⋮n-5\)
\(\Leftrightarrow2n-10+19⋮n-5\)
\(\Leftrightarrow n-5\in\left\{1;-1;19;-19\right\}\)
hay \(n\in\left\{6;4;29;-14\right\}\)
4 tháng 7 2023
=>6n+2 chia hết cho 2n+3
=>6n+9-7 chia hết cho 2n+3
=>2n+3 thuộc Ư(-7)
mà n là số tự nhiên
nên 2n+3=7
=>2n=4
=>n=2
AA
0
5 tháng 2 2022
Bài 2:
a: \(\Leftrightarrow3n-3+10⋮n-1\)
\(\Leftrightarrow n-1\in\left\{-1;1;2;5;10\right\}\)
hay \(n\in\left\{0;2;3;6;11\right\}\)
b: \(\Leftrightarrow n^2-1+9⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;3;9\right\}\)
hay \(n\in\left\{0;2;8\right\}\)
RA
1
MV
11 tháng 1 2018
\(3n+2=3n-12+14=\left(-3\right)\left(4-n\right)+14\\ \left(-3\right)\left(4-n\right)⋮4-n\\ \text{Để }3n+2⋮4-n\Rightarrow14⋮4-n\Rightarrow4-n\inƯ\left(14\right)=\left\{-14;-7;-2;-1;1;2;7;14\right\}\)
| $ 4 - n $ | $ n $ |
| $ - 14 $ | $ 18 $ |
| $ - 7 $ | $ 11 $ |
| $ - 2 $ | $ 6 $ |
| $ - 1 $ | $ 5 $ |
| $ 1 $ | $ 3 $ |
| $ 2 $ | $ 2 $ |
| $ 7 $ | $ - 3 $ |
| $ 14 $ | $ - 10 $ |
Vậy \(n\in\left\{-10;-3;2;3;5;6;11;18\right\}\)
\(n^2+n+2=n^2-1+n-1+4=\left(n+1\right)\left(n-1\right)+\left(n-1\right)+4=\left(n-1\right)\left(n+2\right)+4\\ \left(n-1\right)\left(n+2\right)⋮n-1\\ \text{Để }n^2+n+2⋮n-1\Rightarrow4⋮n-1\Rightarrow n-1\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
| $ n - 1 $ | $ n $ |
| $ - 4 $ | $ - 3 $ |
| $ - 2 $ | $ - 1 $ |
| $ - 1 $ | $ 0 $ |
| $ 1 $ | $ 2 $ |
| $ 2 $ | $ 3 $ |
| $ 4 $ | $ 5 $ |
Vậy \(n\in\left\{-3;-1;0;2;3;5\right\}\)
1
AN
1
10 tháng 2 2019
a) Ta có : n+6 ⋮ n
mà n ⋮ n ⇒ 6 ⋮ n ⇒ n ∈ Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
b) Vì n+5 ⋮ n+1 ⇒ (n+1)+4 ⋮ n+1
mà n+1 ⋮ n+1 ⇒ 4 ⋮ n+1
⇒ n+1 ∈ Ư(4) = { -4; -2; -1; 1; 2; 4}
⇒ n+1 ∈ { -4; -2; -1; 1; 2; 4}
⇒ n ∈ { -5; -3; -2; 0; 1; 3 }
c) Vì 3.8 - 3n ⋮ n
⇒\(\left\{{}\begin{matrix}24⋮n\\3n⋮n\end{matrix}\right.\)
mà 3n ⋮ n ⇒ 24⋮n ⇒ n ∈ Ư(24)
Ư(24) = {-24;-12;-8;-6;-4;-3;-2;-1;1;2;3;4;6;8;12;24}
⇒ n ∈ ...
Mk không chắc chắn lắm, nếu sai thì thôi nhé
5 tháng 11 2016
a.
Ta có: \(405^n=......5\)
\(2^{405}=2^{404}\cdot2=\left(.......6\right)\cdot2=.......2\)
\(m^2\) là số chính phương nên có chữ số tận cùng khác 3. Vậy A có chữ số tận cùng khác 0 \(\Rightarrow A⋮10\)
b.
\(B=\frac{2n+9}{n+2}+\frac{5}{n+2}\frac{n+17}{ }-\frac{3n}{n+2}=\frac{2n+9+5n+17-3n}{n+2}=\frac{4n+26}{n+2}\)
\(B=\frac{4n+26}{n+2}=\frac{4\left(n+2\right)+18}{n+2}=4+\frac{18}{n+2}\)
Để B là số tự nhiên thì \(\frac{18}{n+2}\) là số tự nhiên
\(\Rightarrow18⋮\left(n+2\right)\Rightarrow n+2\inư\left(18\right)=\left\{1;2;3;6;9;18\right\}\)
+ \(n+2=1\Leftrightarrow n=-1\) ( loại )
+ \(n+2=2\Leftrightarrow n=0\)
+ \(n+2=3\Leftrightarrow n=1\)
+ \(n+2=6\Leftrightarrow n=4\)
+ \(n+2=9\Leftrightarrow n=7\)
+ \(n+2=18\Leftrightarrow n=16\)
Vậy \(n\in\left\{0;1;4;7;16\right\}\) thì \(B\in N\)
c.
Ta có \(55=5\cdot11\) mà \(\left(5;1\right)=1\)
Do đó \(C=\overline{x1995y}⋮55\)\(\Leftrightarrow\)\(\begin{cases}C⋮5\\C⋮11\end{cases}\) \(\frac{\left(1\right)}{\left(2\right)}\)
\(\left(1\right)\Rightarrow y=0\) hoặc \(y=5\)
+ \(y=0\div\left(2\right)\Rightarrow x+9+5-\left(1+9+0\right)⋮11\Rightarrow x=7\)
+ \(y=5\div\left(2\right)\Rightarrow x+9+5-\left(1+9+5\right)⋮11\Rightarrow x=1\)
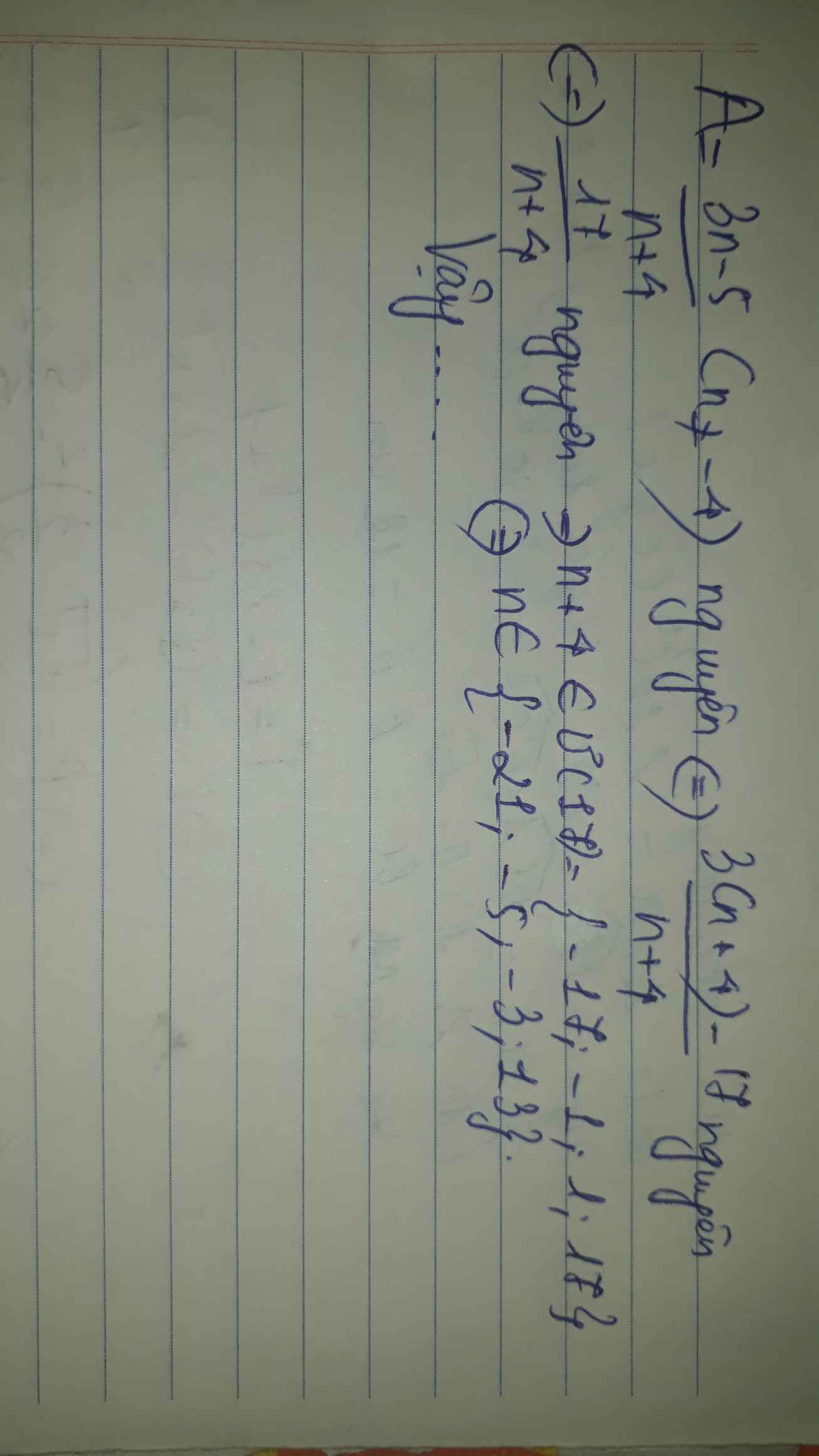
\(3n+2⋮n-2\)
=>\(3n-6+8⋮n-2\)
=>\(8⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
=>\(n\in\left\{3;1;4;0;6;-2;10;-6\right\}\)
mà n>=0
nên \(n\in\left\{3;1;4;0;6;10\right\}\)
=0