
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)

bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với

c: \(y=-x^2+2x+3\)
=>\(y^{\prime}=-2x+2\)
Đặt y'<0
=>-2x+2<0
=>-2x<-2
=>x>1
=>Hàm số nghịch biến trên (1;+∞)
Đặt y'>0
=>-2x+2>0
=>-2x>-2
=>x<1
=>Hàm số đồng biến trên (-∞;1)
d: \(y=\frac13x^3+3x^2+5x+2\)
=>\(y^{\prime}=\frac13\cdot3x^2+3\cdot2x+5=x^2+6x+5=\left(x+1\right)\left(x+5\right)\)
Đặt y'>0
=>(x+1)(x+5)>0
=>\(\left[\begin{array}{l}x>-1\\ x<-5\end{array}\right.\)
=>Hàm số đồng biến trên các khoảng (-1;+∞) và (-∞;-5)
Đặt y'<0
=>(x+1)(x+5)<0
=>-5<x<-1
=>Hàm số nghịch biến trên khoảng (-5;-1)


nhờ người ta giải mà cười hihi
em thì bó tay chấm chữ com vào ăn
TXĐ: D=R
\(9^{x^2+x-1}-10.3^{x^2+x-2}+1=0\)
\(\Leftrightarrow9^{x^2+x-1}-10.\frac{3^{x^2+x-1}}{3}+1=0\)
Đặt t = \(3^{x^2+x-1}\) (t>0)
\(\Leftrightarrow t^2-\frac{10}{3}t+1=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}t=3\\t=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}3^{x^2+x-1}=3\\3^{x^2+x-1}=\frac{1}{3}\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2+x-1=1\\x^2+x-1=\frac{1}{3}\end{array}\right.\)
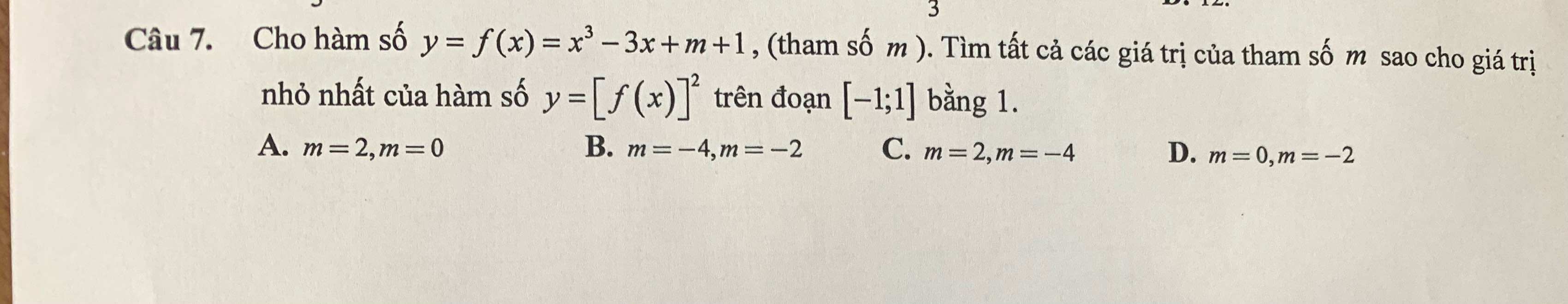








Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
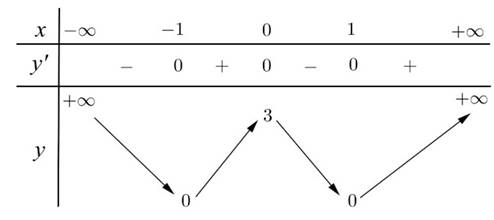
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
=5145484985742651291274572147214912742724765142721567