NQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
2 tháng 1 2019
Vì các nghiệm của phương trình thuộc khoảng
(
0
;
2
π
)
nên nghiệm của phương trình là 
CM
6 tháng 6 2019
Chọn A
Ta có sin3x+ cos2x- sinx= 0 ⇔ cos2x(2sinx+1)=0. Lưu ý trong khoảng (0;π), sinx > 0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2020
Bài này sử dụng kiến thức 12 thì rất dễ chứ lớp 11 thì đúng là chẳng biết biện luận thế nào
Y
1
AH
Akai Haruma
Giáo viên
7 tháng 10 2021
Lời giải:
\(\sin 3x=-\sin x=\sin (-x)\)
\(\Leftrightarrow \left[\begin{matrix} 3x=-x+2k\pi\\ 3x=\pi +x+2t\pi\end{matrix}\right.\) với $t,k$ nguyên bất kỳ
\(\Leftrightarrow \left[\begin{matrix} x=\frac{k\pi}{2}\\ x=\frac{(2t+1)\pi}{2}\end{matrix}\right.\) với $k,t$ nguyên bất kỳ
Để $x\in [0; 100\pi]$ thì \(\left\{\begin{matrix} 0\leq \frac{k}{2}\leq 100\\ 0\leq \frac{2t+1}{2}\leq 100\end{matrix}\right.\)
Vì $t,k$ nguyên nên:
$k\in \left\{0;1;2;...;200\right\}$ $\rightarrow 201$ giá trị
$t\in \left\{0;1;2;,,,;99\right\}$ $\rightarrow 100$ giá trị
Vậy có: $201+100=301$ nghiệm.
HT
17 tháng 8 2019
1/ ĐKXĐ: \(\cos2x\ne0\)
\(\frac{\cos4x}{\cos2x}=\frac{\sin2x}{\cos2x}\)\(\Leftrightarrow\cos4x-\sin2x=0\)
\(\Leftrightarrow2\cos^22x-1-\sin2x=0\)
\(\Leftrightarrow2-2\sin^22x-1-\sin2x=0\)
\(\Leftrightarrow2\sin^22x+\sin2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\frac{1}{2}=\sin\frac{\pi}{6}\\\sin2x=-1=\sin\frac{-\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{6}+2k\pi\\2x=\frac{5\pi}{6}+2k\pi\\2x=\frac{-\pi}{2}+2k\pi\left(l\right)\\2x=\frac{3\pi}{2}+2k\pi\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+k\pi\\x=\frac{5\pi}{12}+k\pi\end{matrix}\right.\)
HT
17 tháng 8 2019
2/ \(\sin2.4x+\cos4x=1+2\sin2x.\cos\left(2x+4x\right)\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+2\sin2x.\left(\cos2x.\cos4x-\sin2x.\sin4x\right)\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+2\sin2x.\cos2x.\cos4x-2\sin^22x.\sin4x\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+\sin4x.\cos4x-\sin4x+\cos4x.\sin4x\)
Đến đây bn tự giải nốt nhé, lm kiểu bthg thôi bởi vì đã quy về hết sin4x và cos4x r
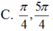
\(sin3x+sinx=0\)
\(\Leftrightarrow3sinx-4sin^3x+sinx=0\)
\(\Leftrightarrow sinx\left(4-4sin^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=1\\sinx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{2}+2k\pi\\x=-\dfrac{\pi}{2}+2k\pi\end{matrix}\right.\left(k\inℤ\right)\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\left(k\inℤ\right)\)
Vậy pt đã cho có tập nghiệm là \(S=\left\{\dfrac{k\pi}{2}|k\inℤ\right\}\)
Cho \(-2021\pi\le\dfrac{k\pi}{2}\le2021\pi\Leftrightarrow-4042\le k\le4042\), mà \(k\inℤ\) nên có tổng cộng là \(8085\) nghiệm.