Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

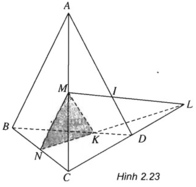
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.
Gọi L = NK ∩ CD
Ta có L ∈ NK ⇒ L ∈ (MNK)
L ∈ CD ⇒ L ∈ (ACD)
Nên ML = (ACD) ∩ (MNK) = Δ
Δ ∩ AD = I ⇒ I = (MNK) ∩ AD

Đáp án C
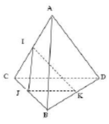
Mặt phẳng (ABD) cắt mặt phẳng (IJK) theo giao tuyến song song với AB do IJ//AB

Trong mp(BCD), gọi M là giao điểm của KJ với DC
\(M\in KJ\subset\left(IJK\right)\)
\(M\in CD\subset\left(ACD\right)\)
Do đó: \(M\in\left(IJK\right)\cap\left(ACD\right)\left(1\right)\)
\(I\in AC\subset\left(ACD\right);I\in\left(IJK\right)\)
=>\(I\in\left(ACD\right)\cap\left(IJK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(IJK\right)\cap\left(ACD\right)=MI\)
Xét ΔCAB có
\(\dfrac{CI}{CA}=\dfrac{CJ}{CB}=\dfrac{1}{2}\)
nên IJ//AB
\(K\in BD\subset\left(ABD\right);K\in\left(IJK\right)\)
=>\(K\in\left(ABD\right)\cap\left(IJK\right)\)
Xét (ABD) và (IJK) có
\(K\in\left(ABD\right)\cap\left(IJK\right)\)
IJ//AB
Do đó: (ABD) giao (IJK)=xy, xy đi qua K và xy//IJ//AB

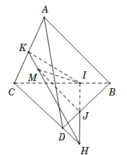
Trong mặt phẳng (BCD); IJ cắt CD tại H nên H thuộc (ACD)
Điểm H thuộc IJ m suy ra bốn điểm M; I; J; H đồng phẳng.
Nên trong mặt phẳng (IJM) , MH cắt IJ tại H và M H ⊂ I J M .
Mặt khác M ∈ A C D H ∈ A C D ⇒ M H ⊂ A C D .
Vậy giao tuyến của 2 mặt phẳng (ACD) và ( IJM) là MH
Chọn D.

Tham khảo:

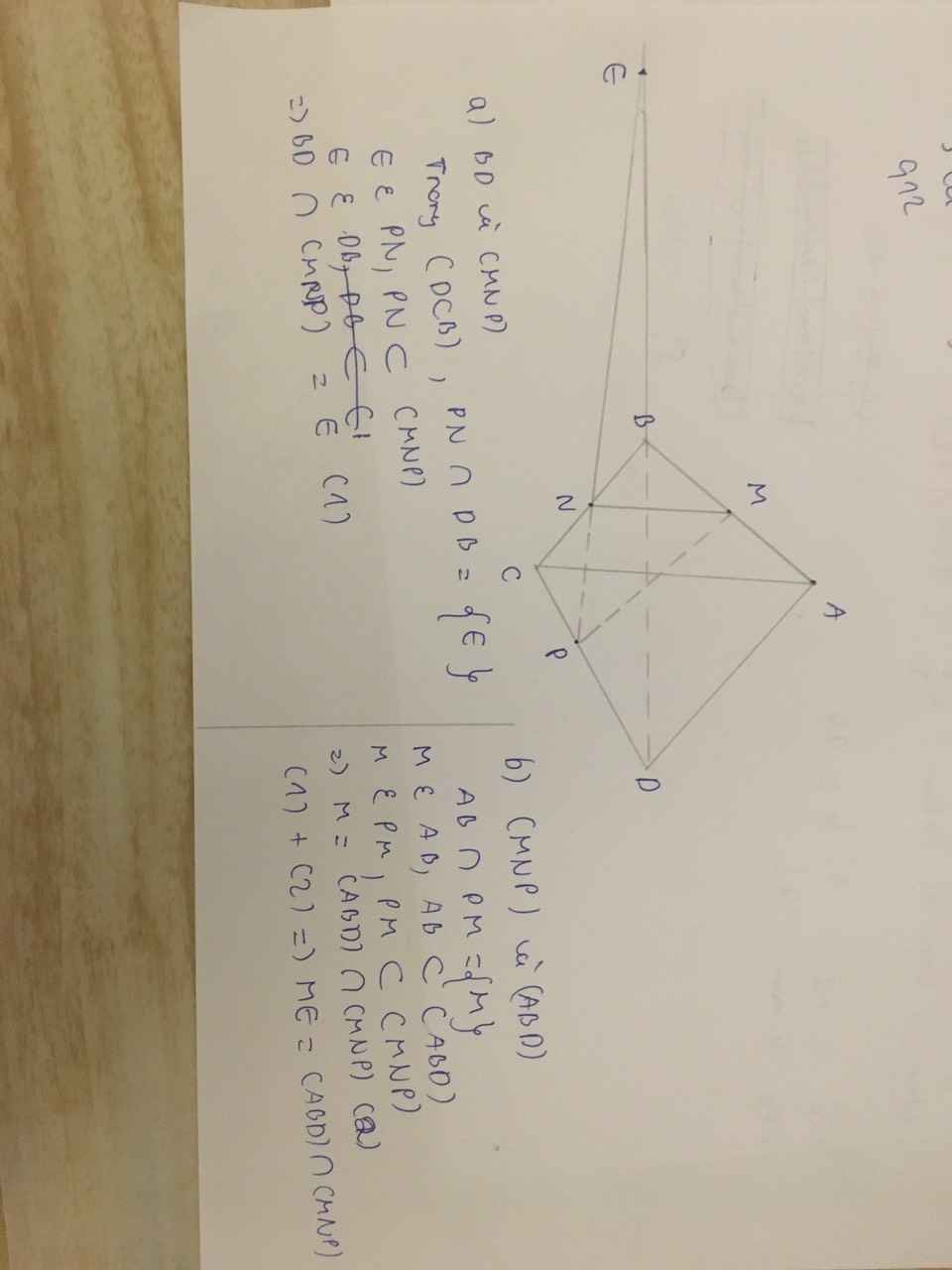
a) Xét trên mp(BCD): NP cắt CD tại I
I thuộc NP suy ra I nằm trên mp(MNP)
Suy ra giao điểm của CD và mp(MNP) là I
b) Ta có I, M đều thuộc mp(ACD) suy ra IM nằm trên mp(ACD)
I, M đều thuộc mp(MNP) suy ra IM nằm trên mp(MNP)
Do đó, IM là giao tuyến của 2 mp(ACD) và mp(MNP) hay EM là giao tuyến của 2 mp(ACD) và mp(MNP).

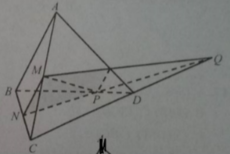
Trong mặt phẳng (DAB), cho AD cắt MK tại E. Trong mặt phẳng (DBC), CD cắt NK tại F.
Khi đó \(E\in AD\subset\left(ACD\right)\) và \(E\in MK\subset\left(MNK\right)\) nên \(E\in\left(ACD\right)\cap\left(MNK\right)\) hay E thuộc giao tuyến của (ACD) và (MNK)
Tương tự, ta có F thuộc giao tuyến của (ACD) và (MNK)
\(\Rightarrow\) EF là giao tuyến của (ACD) và (MNK)
Có \(M\in AB\subset\left(ABD\right)\) và \(M\in MK\subset\left(MNK\right)\) nên M thuộc giao tuyến của (ABD) và (MNK)
\(K\in BD\subset\left(ABD\right)\) và \(K\in KM\subset\left(MNK\right)\) nên K thuộc giao tuyến của (ABD) và (MNK)
Vậy MK là giao tuyến của (ABD) và (MNK)